Vorlesung
Optimierung und inverse Probleme
Prof. Dr. Bastian von Harrach
M. Sc. Tim Jahn
Wintersemester 2018/19
Aktuelles - Inhalt und Ziele - Personen - Termine - Materialien - Literatur - Modulzuordnung
Aktuelles
- Die Nachklausureinsicht findet am Montag, den 15.4. von 11:45-12:15 Uhr im Büro des Übungsleiters 103a statt.
- Die Nachklausur findet am 11.4.2019 von 10-12 s.t. statt, in der Robert-Mayer-Str. 10 / Gräfstr. 38 - RM10 - 110. Teilnahmeberechtigt sind nicht erfolgreiche oder durch ärztlichen Attest entschuldigte Teilnehmer der Erstklausur.
- Die Klausureinsicht findet am Montag, den 18.2 von 10:30-11:00 Uhr in Raum 110 statt.
- Die Übungen am Dienstag, den 27.11.2018 entfallen. Es gibt deswegen ein umfangreicheres Übungsblatt mit einem Bearbeitungszeitraum von zwei Wochen.
- Die Übungsanmeldung findet in der ersten Vorlesung statt.
- Die Übungen zur Vorlesung beginnen in der zweiten Vorlesungswoche.
- Für Fragen oder nachträgliche Anmeldung zum Übungsbetrieb wenden Sie sich bitte an den Übungsleiter.
Inhalt und Ziele
Die Natur- und Wirtschaftswissenschaften wurden in den letzten Jahrzenten revolutioniert durch die Möglichkeit, das Verhalten eines Systems bei vollständiger Kenntnis aller dazu nötigen Parameter rechnergestützt (numerisch) vorherzusagen. Ziel der numerischen Simulation ist oft die Optimierung des Systems oder die Identifikation der beschreibenden Parameter. In dieser Vorlesung wird eine Einführung in (kontinuierliche) Optimierungs- und Identifikationsalgorithmen gegeben. Vorkenntnisse über Optimierung werden nicht vorausgesetzt. Die Vorlesung richtet sich an Bachelor-Studenten ab dem 4. Semester und an Master-Studenten.
 |
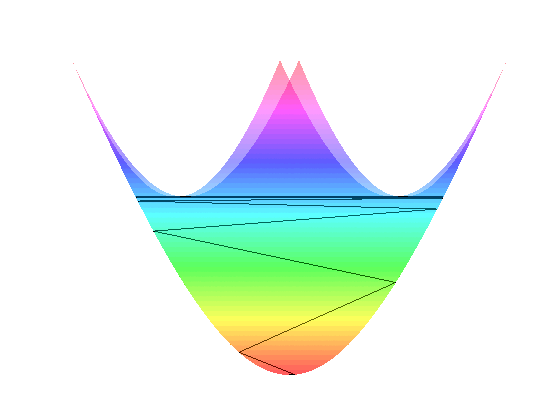 |
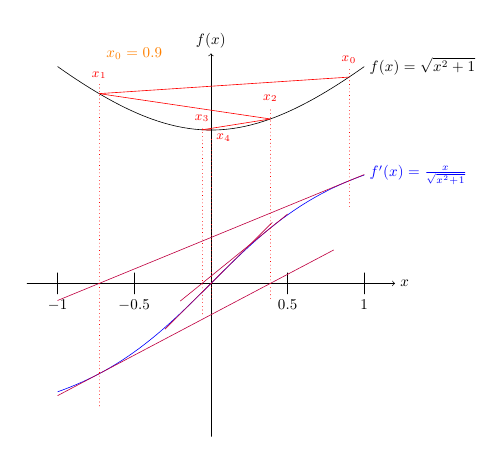
Minimierung einer Zielfunktion durch Anwendung des Newton-Verfahrens auf ihre Ableitung.
Personen
- Prof. Dr. Bastian von Harrach (Dozent)
- M. Sc. Tim Jahn (Übungsleiter)
Termine
Vorlesung
- Dienstags, 10-12 Uhr, Robert-Mayer-Str. 10 / Gräfstr. 38 - RM10 - 109c (10:00-11:40 mit 10 Minuten Pause)
- Donnerstags, 10-12 Uhr, Robert-Mayer-Str. 10 / Gräfstr. 38 - RM10 - 109c (10:15-12:00 mit 15 Minuten Pause)
Übungen
- Dienstags, 8-10 Uhr, Robert-Mayer-Str. 10 / Gräfstr. 38 - RM10 - 110
- Dienstags, 12-14 Uhr, Robert-Mayer-Str. 10 / Gräfstr. 38 - RM10 - 110
- Abhängig von der Teilnehmerzahl werden die Gruppen eventuell zusammengelegt.
Prüfung
- Die Nachklausur findet am 11.4.2019 von 10-12 s.t. statt, in der Robert-Mayer-Str. 10 / Gräfstr. 38 - RM10 - 110. Teilnahmeberechtigt sind nicht erfolgreiche oder durch ärztlichen Attest entschuldigte Teilnehmer der Erstklausur.
- Die Klausur findet am letzen regulären Vorlesungstermin, d.h. am 14.02.2019 von 10-12 Uhr s.t. im Hörsaaltrakt Bockenheim - H7 statt. Die Berabeitungszeit beträgt 90 Minuten.
- Für die Klausur sind alle unbelebten, nicht elektronischen Hilfsmittel und ein nicht programmierbarer Taschenrechner zugelassen.
- Nach §25(4) der Prüfungsordnung erfolgt die offizielle Meldung zur Modulprüfung durch Antritt. Bitte beachten Sie aber, dass bei Nicht-Antritt ohne triftigen Grund nicht an der Wiederholungsprüfung zu Beginn des Sommersemesters 2019 teilgenommen werden darf.
- Für die Zulassung zur Modulprüfung sind keine Studienleistungen erforderlich. Wir empfehlen jedoch, die Modulprüfung nur dann abzulegen, wenn Sie in den Übungen 50% der Punkte in den schriftlichen Aufgaben und den Programmieraufgaben erreicht, 50% der Übungsaufgaben votiert, und zweimal vorgerechnet haben.
Materialien
- Vorlesungsskript (vorläufig, wird während der Vorlesung laufend ergänzt und korrigiert)
- Videoaufzeichnungen der Vorlesung
- Vorlesungsevaluation
Übungsblätter:
- Blatt 1 (Lösungsvorschlag Programmieraufgabe)
- Blatt 2 (Lösungsvorschlag Programmieraufgabe)
- Blatt 3 (Lösungsvorschlag Programmieraufgabe)
- Blatt 4 Lösungsvorschlag Programmieraufgabe)
- Blatt 5 (Lösungsvorschlag Programmieraufgabe)
- Blatt 6 und Blatt 7 (Lösungsvorschlag Programmieraufgabe)
- Blatt 8 (Lösungsvorschlag Programmieraufgabe)
- Blatt 9 (Lösungsvorschlag Programmieraufgabe)
- Blatt 10 (Lösungsvorschlag Programmieraufgabe)
- Blatt 11 (Lösungsvorschlag Programmieraufgabe)
- Blatt 12 (Lösungsvorschlag Programmieraufgabe)
- Blatt 13
Literatur
- M. Ulbrich, S. Ulbrich: Nichtlineare Optimierung, Birkhäuser Basel 2012
- C. Geiger, C. Kanzow: Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben, Springer 1999
- C. Geiger, C. Kanzow: Theorie und Numerik restringierter Optimierungsaugaben, Springer 2002
- M. Hanke-Bourgeois: Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens, Teubner Verlag, Wiesbaden, 2009
Modulzuordnung
- Modulkürzel: BaM-NUM-g, BaM-NUM-gs, MaM-FN-g, MaM-FN-gs
- Link zur Veranstaltungsseite im Vorlesungsverzeichnis: Vorlesung & Übung.





