Quantum Matter Theory Group

Welcome to the homepage of our group! Our research is focused on ultracold gases in optical lattices, hybrid quantum simulators such as ion-atom systems, and strongly correlated electrons, e.g. in nanostructures. You can find descriptions of the individual research projects here. Below is a selection of recent publications.
Research News
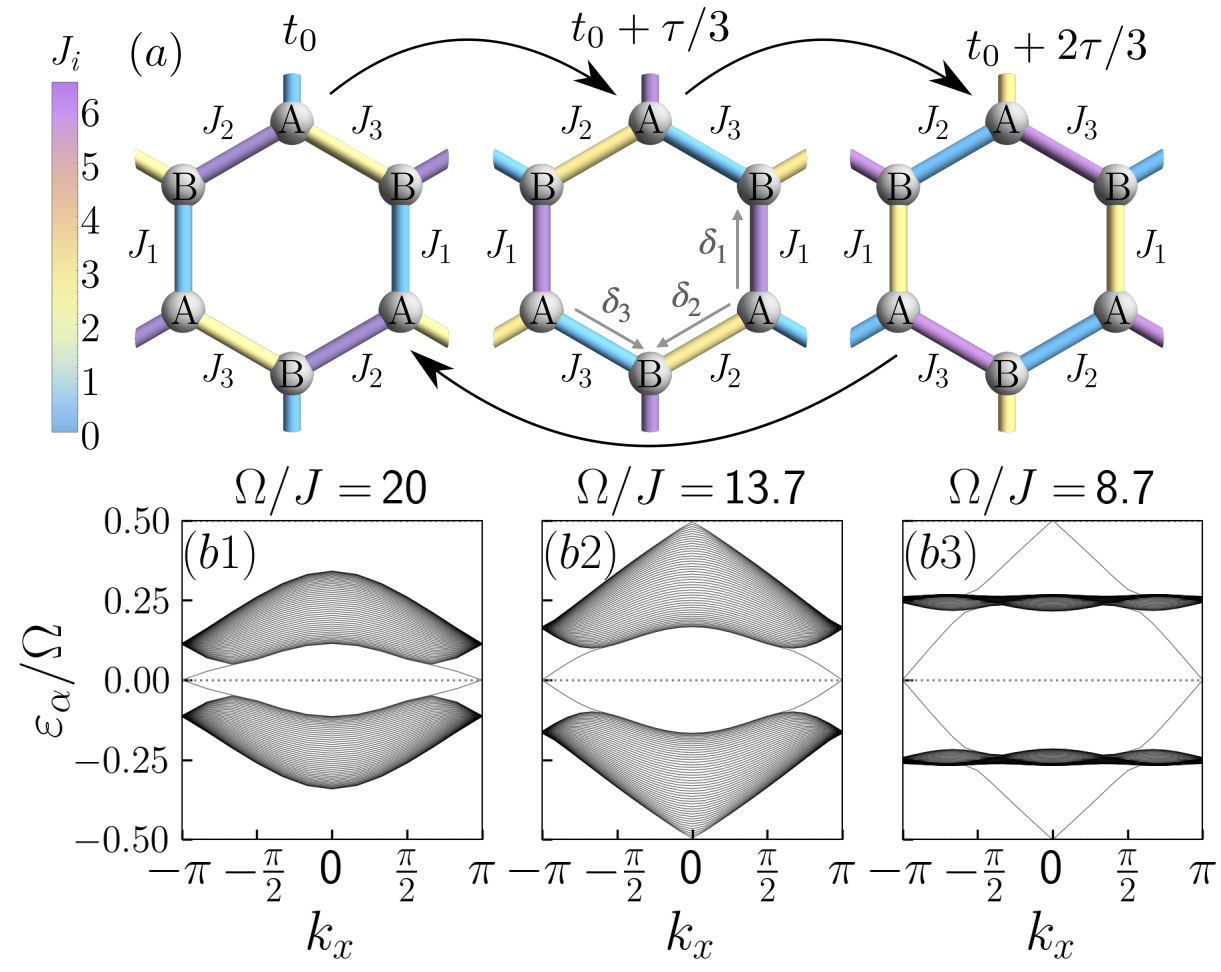 The anomalous Floquet Anderson insulator in a continuously driven optical lattice
The anomalous Floquet Anderson insulator in a continuously driven optical lattice
(arXiv:2312.13589, Phys. Rev. B 109, L121114 (2024))
The anomalous Floquet Anderson insulator (AFAI) has been theoretically predicted in step-wise periodically driven models, but its stability under more general driving protocols hasn't been determined. We show that adding disorder to the anomalous Floquet topological insulator realized with a continuous driving protocol in the experiment by K. Wintersperger et. al., Nat. Phys. 16, 1058 (2020), supports an AFAI phase, where, for a range of disorder strengths, all the time averaged bulk states become localized, while the pumped charge in a Laughlin pump setup remains quantized.
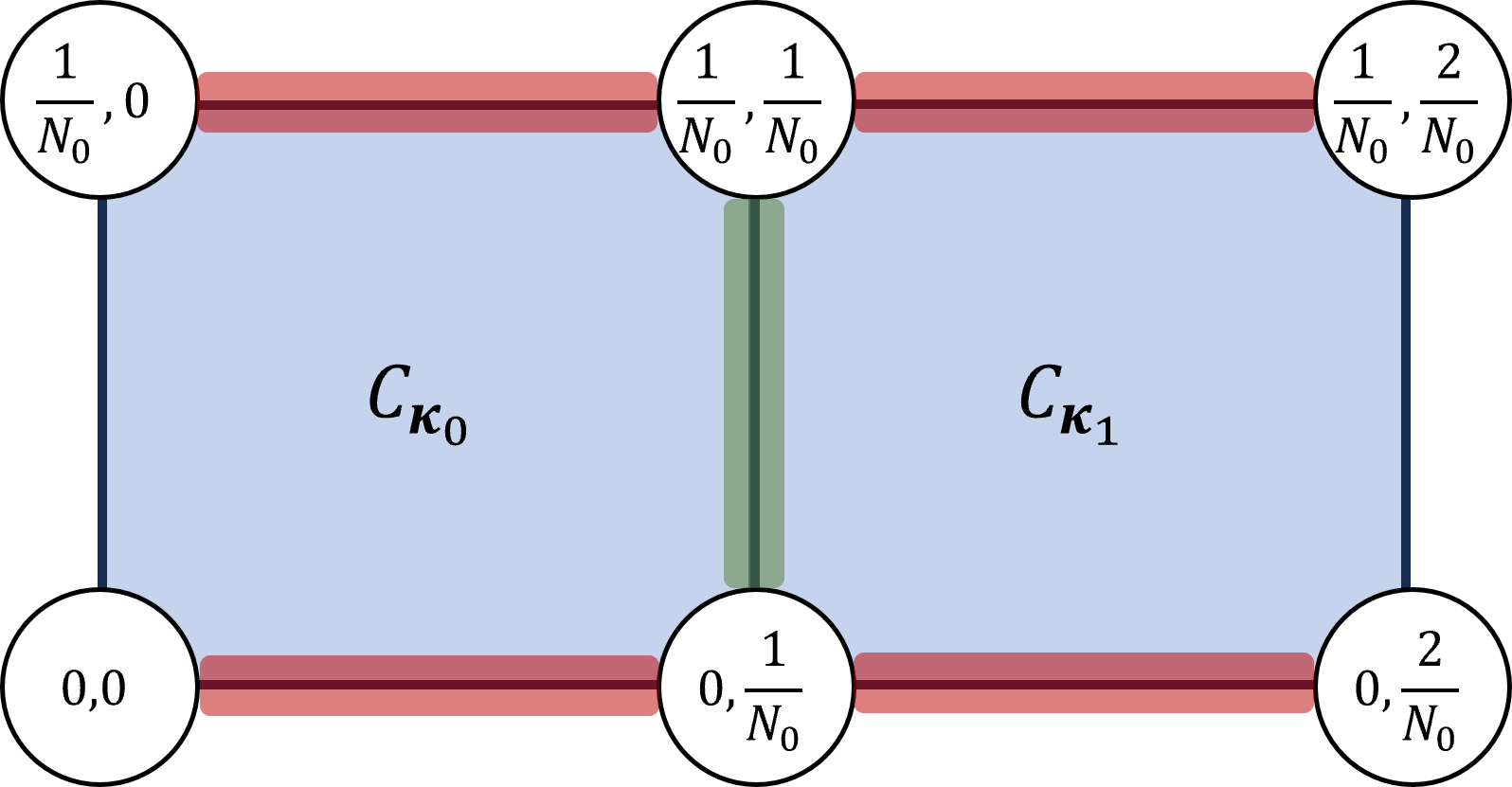 Getting topological invariants from snapshots: a protocol for defining and calculating topological invariants of systems with discrete parameter space
Getting topological invariants from snapshots: a protocol for defining and calculating topological invariants of systems with discrete parameter space
(arXiv:2311.11618)
Topological invariants, including the Chern numbers, can topologically classify parameterized Hamiltonians. We find that topological invariants can be properly defined and calculated even if the parameter space is discrete, which is done by geodesic interpolation in the classifying space. We specifically present the interpolation protocol for the Chern numbers, which can be directly generalized to other topological invariants. The protocol generates a highly efficient algorithm for numerical calculation of the second and higher Chern numbers, by which arbitrary precision can be achieved given the values of the parameterized Hamiltonians on a coarse grid with a fixed resolution in the parameter space. Our findings also open up opportunities to study topology in finite-size systems where the parameter space can be naturally discrete.
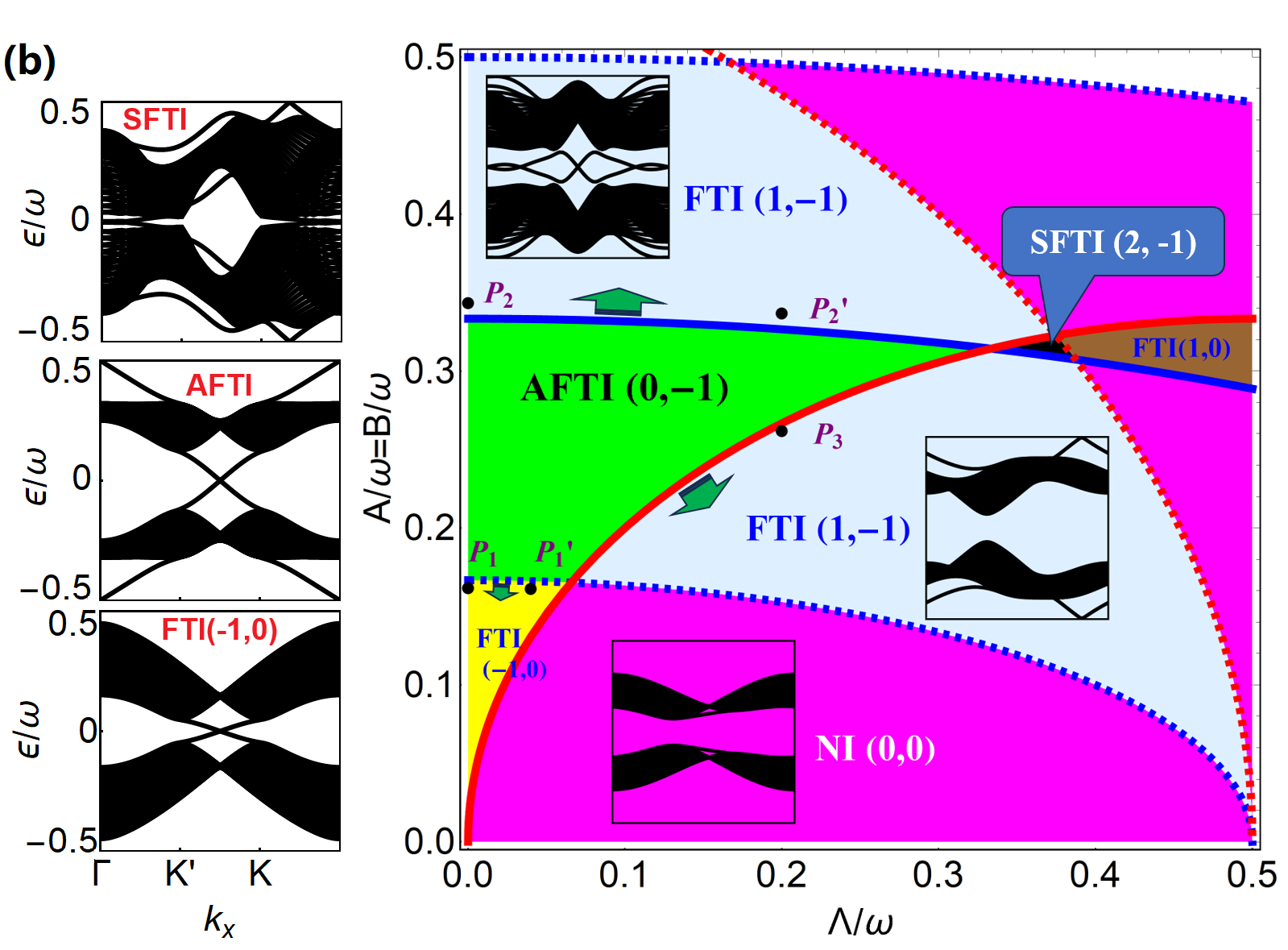 Floquet topological phase transitions induced by uncorrelated or correlated disorder
Floquet topological phase transitions induced by uncorrelated or correlated disorder
(arXiv:2309.07035)
The impact of weak disorder and its spatial correlation on the topology of a Floquet system is not well understood so far. In this study, we investigate a model closely related to a two-dimensional Floquet system that has been realized in experiments. In the absence of disorder, we determine the phase diagram and identify a new phase characterized by edge states with alternating chirality in adjacent gaps. When weak disorder is introduced, we examine the disorder-averaged Bott index and analyze why the anomalous Floquet topological insulator is favored by both uncorrelated and correlated disorder, with the latter having a stronger effect. For a system with a ring-shaped gap, the Born approximation fails to explain the topological phase transition, unlike for a system with a point-like gap.
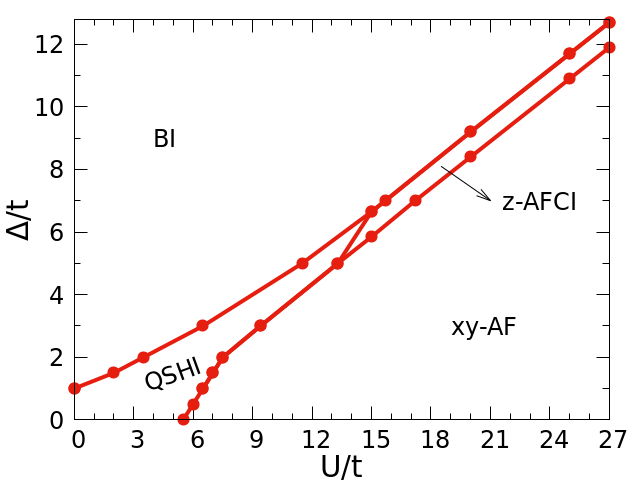 Antiferromagnetic Chern insulator in centrosymmetric systems
Antiferromagnetic Chern insulator in centrosymmetric systems
(arXiv:2209.04730, Phys. Rev. B 106, 205107 (2022))
An antiferromagnetic Chern insulator (AFCI) can exist if the effect of the time-reversal transformation on the electronic state cannot be compensated by a space group operation. The AFCI state with collinear magnetic order is already realized in noncentrosymmetric honeycomb structures through the Kane-Mele-Hubbard model. In this paper, we demonstrate the existence of the collinear AFCI in a square lattice model which preserves the inversion symmetry. Our study relies on the time-reversal-invariant Harper-Hofstadter-Hubbard model extended by a next-nearest-neighbor hopping term including spin-orbit coupling and a checkerboard potential. We show that an easy z-axis AFCI appears between the band insulator at weak and the easy xy-plane AF Mott insulator at strong Hubbard repulsion provided the checkerboard potential is large enough. The close similarity between our results and the results obtained for the noncentrosymmetric Kane-Mele-Hubbard model suggests the AFCI as a generic consequence of spin-orbit coupling and strong electronic correlation which exists beyond a specific model or lattice structure. An AFCI with the electronic and the magnetic properties originating from the same strongly interacting electrons is promising candidate for a strong magnetic blue shift of the charge gap below the Néel temperature and for realizing the quantum anomalous Hall effect at higher temperatures so that applications for data processing become possible.
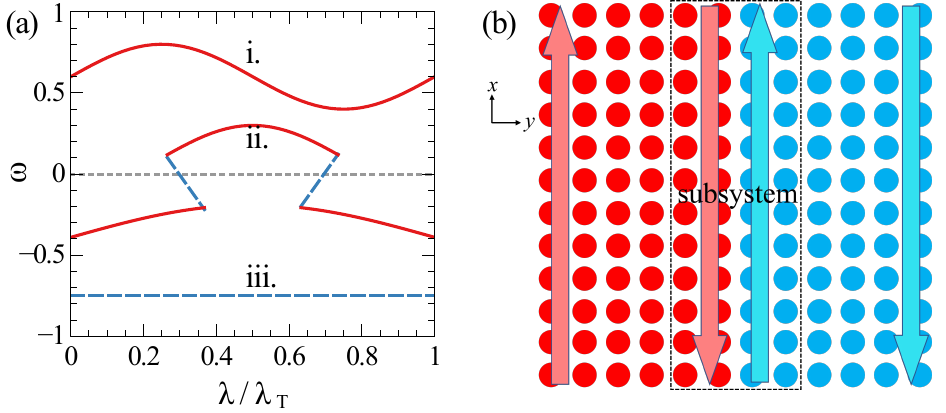 Invisible flat bands on a topological chiral edge
Invisible flat bands on a topological chiral edge
(arXiv:2204.11946, Phys. Rev. B 106, L22047 (2022))
We prove that invisible bands associated with zeros of the single-particle Green's function exist ubiquitously at topological interfaces of 2D Chern insulators, dual to the chiral edge/domain-wall modes. We verify this statement in a repulsive Hubbard model with a topological flat band, using real-space dynamical mean-field theory to study the domain walls of its ferromagnetic ground state. Moreover, our numerical results show that the chiral modes are split into branches due to the interaction, and that the branches are connected by invisible flat bands. Our work provides deeper insight into interacting topological systems.
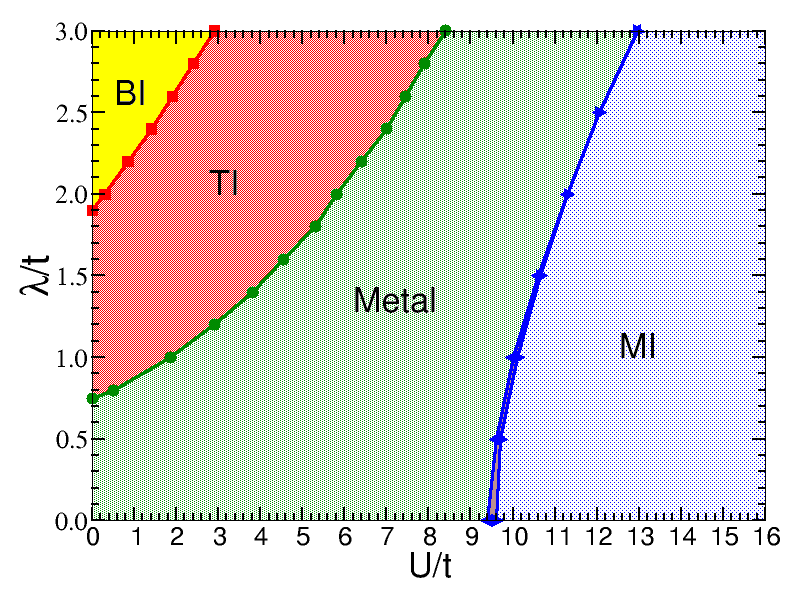 Hubbard model on the kagome lattice with time-reversal invariant flux and spin-orbit coupling
Hubbard model on the kagome lattice with time-reversal invariant flux and spin-orbit coupling
(arXiv:2204.01350, Phys. Rev. B 105, 235102 (2022))
We study the Hubbard model with time-reversal invariant flux and spin-orbit coupling and position-dependent onsite energies on the kagome lattice, using numerical and analytical methods. In particular, we perform calculations using real space dynamical mean-field theory (R-DMFT). To study the topological properties of the system, we use the topological Hamiltonian approach. We obtain a rich phase diagram: for weak and intermediate interactions, depending on the model parameters, the system is in the band insulator, topological insulator, or metallic phase, while for strong interactions the system is in the Mott insulator phase. We also investigate the magnetic phases that occur in this system. For this purpose, in addition to R-DMFT, we also use two analytical methods: perturbation theory for large interactions and onsite energies, and stochastic mean-field theory.
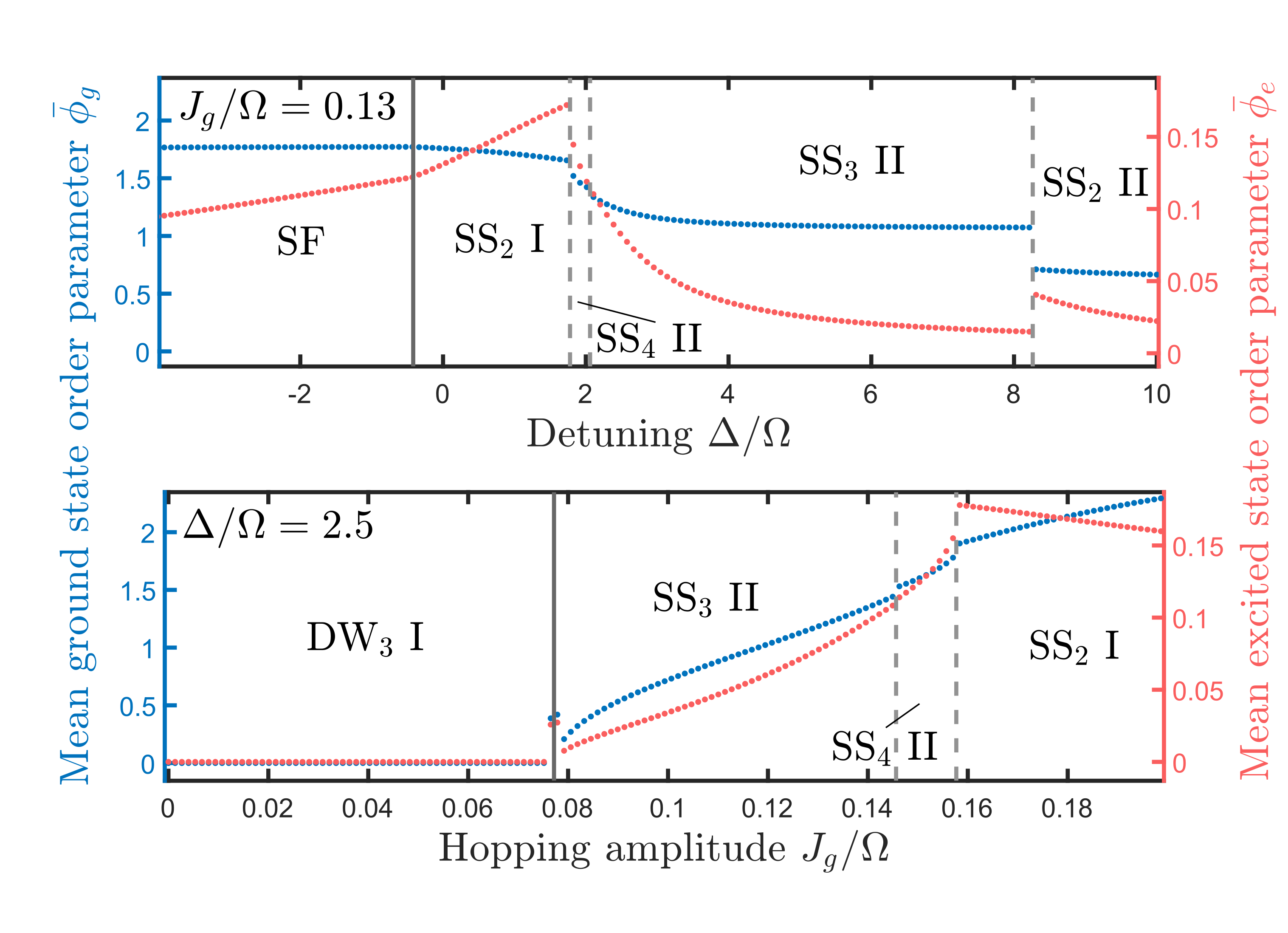 Supersolid phases of ultracold bosons trapped in optical lattices dressed with Rydberg p-states
Supersolid phases of ultracold bosons trapped in optical lattices dressed with Rydberg p-states
(arXiv:2109.04917, Phys. Rev. A 105, 013326 (2022))
Engineering quantum phases with spontaneously broken symmetries is a major goal of research in different fields. Trapped ultracold Rydberg-excited atoms in optical lattices are a promising platform for realizing quantum phases with broken lattice translational symmetry since they are interacting over distances larger than the lattice constant. Although numerous theoretical works on trapped Rydberg-excited gases have predicted such phases, in particular density wave or supersolid phases, their experimental observation proves to be difficult due to challenges such as scattering processes and the limited experimentally achievable coupling strength. Most of these previous studies have focused on isotropically interacting gases dressed with Rydberg s-states, while the effect of anisotropic interactions due to Rydberg-excited p-states in trapped quantum gases remains much less investigated. Additionally, it was shown that the excitation scheme used to excite Rydberg p-states possesses advantages regarding achievable coupling strengths and limitation of scattering processes compared to its s-state counterpart, which makes the investigation of Rydberg p-state dressed quantum gases even more interesting. In the present work, we study the extended, two-component Bose-Hubbard model, realized with a bosonic quantum gas with Rydberg-excited p-states trapped in an optical lattice, within Gutzwiller mean-field theory. We compute the ground state phase diagram and investigate its different regimes. By comparison to the phase diagram of the isotropic case, we find the anisotropic interaction to be more advantageous for the observation of supersolid phases.
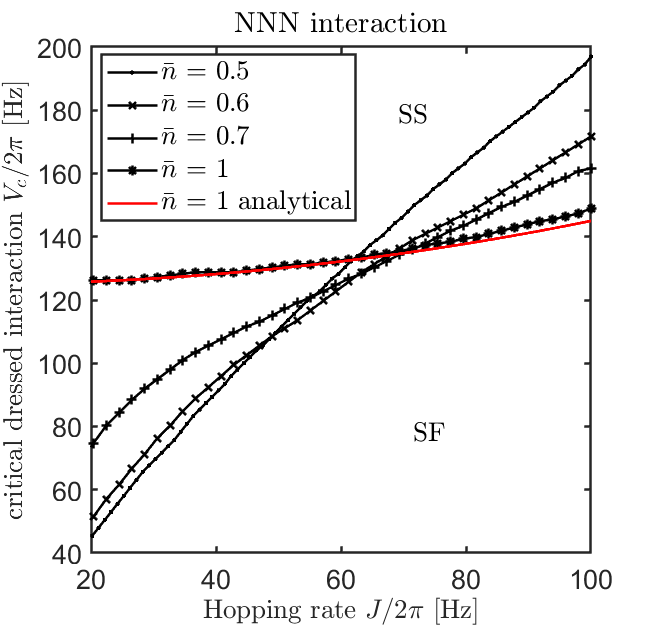 Extended Bose-Hubbard models with Rydberg macrodimer dressing
Extended Bose-Hubbard models with Rydberg macrodimer dressing
(arXiv:2105.15046, Phys. Rev. A 104, 053304 (2021))
Extended Hubbard models have proven to bear novel phases of matter, but their experimental realization remains challenging. In this work we propose to use bosonic quantum gases dressed with molecular bound states in Rydberg interaction potentials for the observation of these quantum states. We study the molecular Rabi coupling with respect to the effective principal quantum number and trapping frequency of the ground-state atoms for various molecular potentials of rubidium and potassium, and the hereby resulting dressed interaction strength. Additionally, we propose a two-color excitation scheme which significantly increases the dressed interaction and cancels otherwise-limiting ac Stark shifts. We study the various equilibrium phases of the corresponding extended Bose-Hubbard model by means of the cluster Gutzwiller approach and perform time evolution simulations via the Lindblad master equation. We find a supersolid phase by slowly ramping the molecular Rabi coupling of an initially prepared superfluid and discuss the role of dissipation.
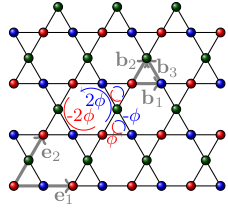 Spin-orbit coupling in the kagome lattice with flux and time-reversal symmetry
Spin-orbit coupling in the kagome lattice with flux and time-reversal symmetry
(arXiv:2101.12219, Phys. Rev. B 103, 195105 (2021))
We study the topological properties of a spin-orbit coupled Hofstadter model on the Kagome lattice. The model is time-reversal invariant and realizes a Z2 topological insulator as a result of artificial gauge fields. We develop topological arguments to describe this system showing three inequivalent sites in a unit cell and a flat band in its energy spectrum in addition to the topological dispersive energy bands. We show the stability of the topological phase towards spin-flip processes and different types of on-site potentials. In particular, we also address the situation where on-site energies may differ inside a unit cell. Moreover, a staggered potential on the lattice may realize topological phases for the half-filled situation. Another interesting result is the occurrence of a topological phase for large on-site energies. To describe topological properties of the system we use a numerical approach based on the twisted boundary conditions and we develop a mathematical approach, related to smooth fields.
 Topological Mott transition in a Weyl-Hubbard model with dynamical mean-field theory
Topological Mott transition in a Weyl-Hubbard model with dynamical mean-field theory
(arXiv:2011.05100, Phys. Rev. B 103, 125132 (2021))
Weyl semimetals are three-dimensional, topologically protected, gapless phases which show exotic phenomena such as Fermi arc surface states or negative magnetoresistance. It is an open question whether interparticle interactions can turn the topological semimetal into a topologically nontrivial Mott insulating phase. We investigate an experimentally motivated model for Weyl physics of cold atoms in optical lattices, with the main focus on interaction effects and topological properties by means of dynamical mean-field theory (DMFT). We characterize topological phases by numerically evaluating the Chern number via the Ishsikawa-Matsuyama formula for interacting phases. Within our studies, we find that the Chern numbers become trivial when interactions lead to insulating behavior. For a deeper understanding of the Weyl-semimetal-to-Mott-insulator topological phase transition, we evaluate the topological properties of quasiparticle bands as well as so-called blind bands. Our study is complementary to recent studies of Weyl semimetals with DMFT.
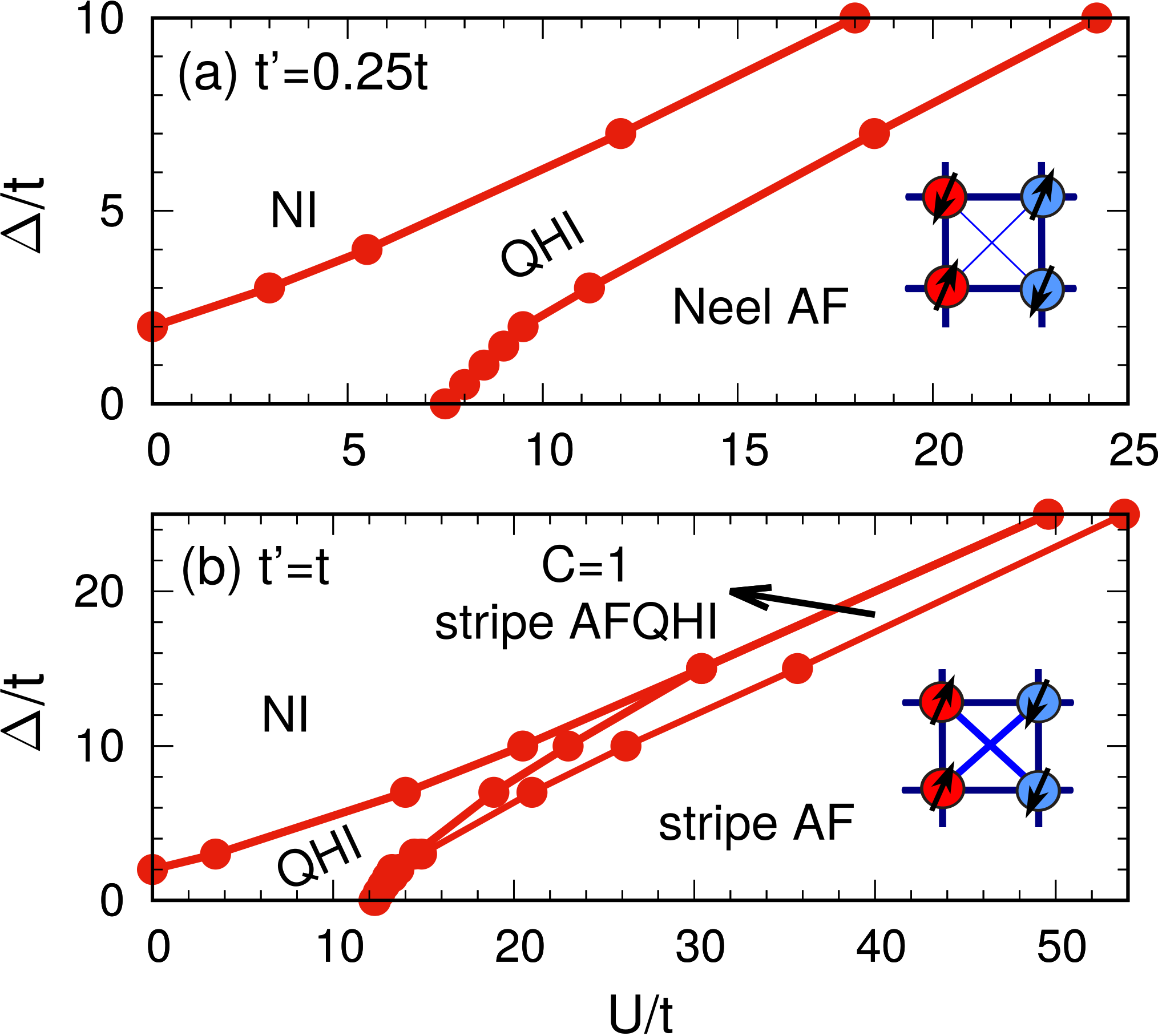 Lattice Symmetry and Emergence of Antiferromagnetic Quantum Hall States
Lattice Symmetry and Emergence of Antiferromagnetic Quantum Hall States
(arXiv:2006.09515, Phys. Rev. B 103, 155108 (2021))
We consider the spinful Harper-Hofstadter model extended by a next-nearest-neighbor (NNN) hopping which opens a gap at half-filling and allows for the realization of a quantum Hall insulator (QHI). The QHI has the Chern number C=2 as both spin components are in the same quantum Hall state. We add to the system a staggered potential Δ along the x-direction favoring a normal insulator (NI) and the Hubbard interaction U favoring a Mott insulator (MI). The MI is a Néel antiferromagnet (AF) for small and a stripe AF for large NNN hopping. We investigate the U-Δ phase diagram of the model for both small and large NNN hoppings. We show that while for large NNN hopping there exists a C=1 stripe antiferromagnetic QHI (AFQHI) in the phase diagram, there is no equivalent C=1 Néel AFQHI at the small NNN hopping. We discuss that a C=1 AFQHI can emerge only if the effect of the spin-flip transformation cannot be compensated by a space group operation.
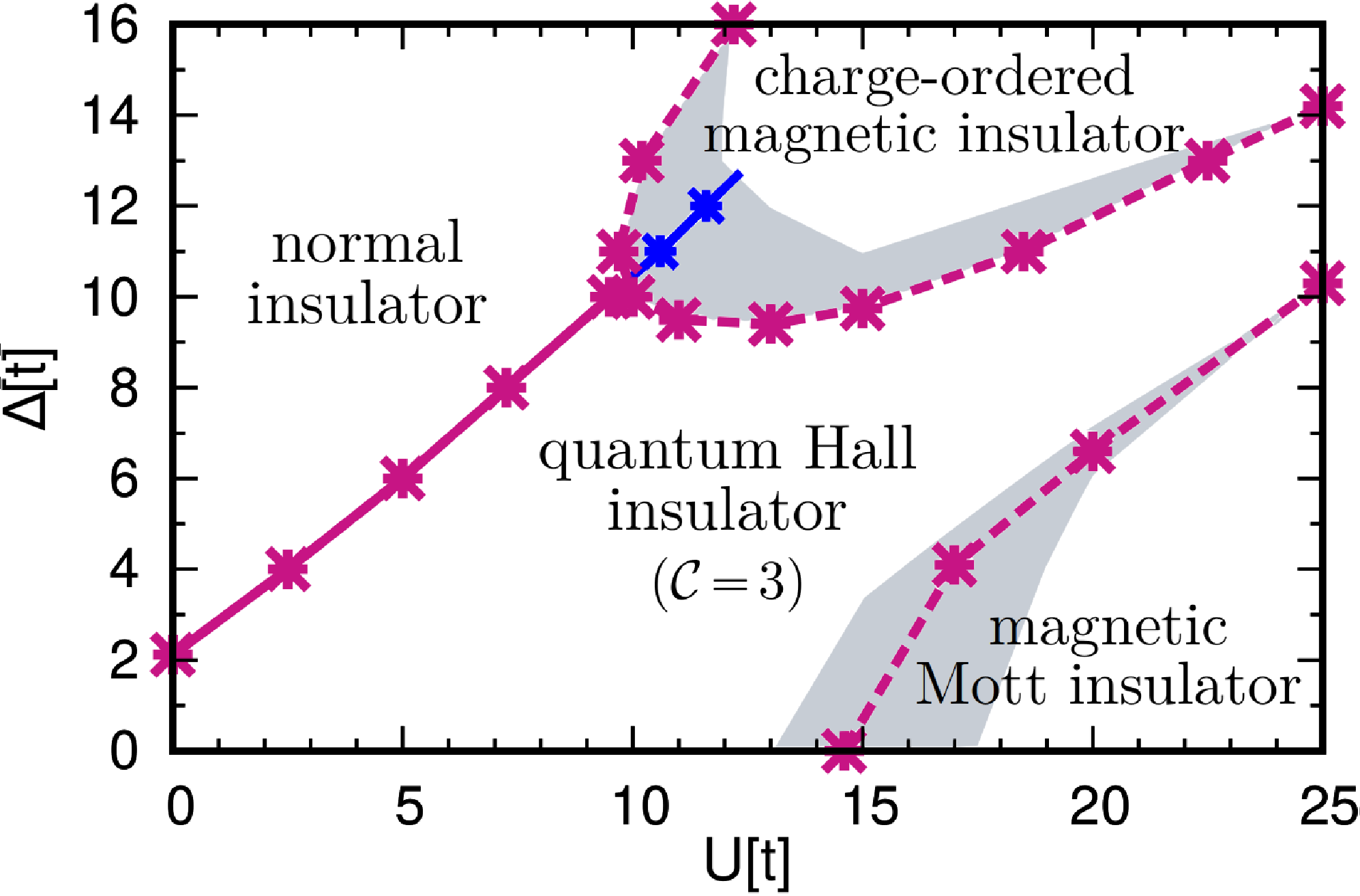 Interaction-Driven Topological Phase Transitions in Fermionic SU(3) Systems
Interaction-Driven Topological Phase Transitions in Fermionic SU(3) Systems
(arXiv:1911.03518, Phys. Rev. B 101, 245159 (2020))
We consider SU(3) fermions on the triangular lattice in the presence of a gauge potential which stabilizes a quantum Hall insulator (QHI) at the density of one particle per lattice site. We investigate the effect of the Hubbard interaction, favoring magnetic long-range order, and a three-sublattice potential (TSP), favoring a normal insulator (NI), on the system. For weak TSP we find that the Hubbard interaction drives the QHI into a three-sublattice magnetic Mott insulator (MMI). For intermediate values of TSP we identify two transition points upon increasing the Hubbard interaction. The first transition is from the NI to the QHI and the second transition is from the QHI to the MMI. For large values of the TSP a charge-ordered magnetic insulator (COMI) emerges between the NI and the QHI, leading to an interaction-driven COMI-to-QHI transition.
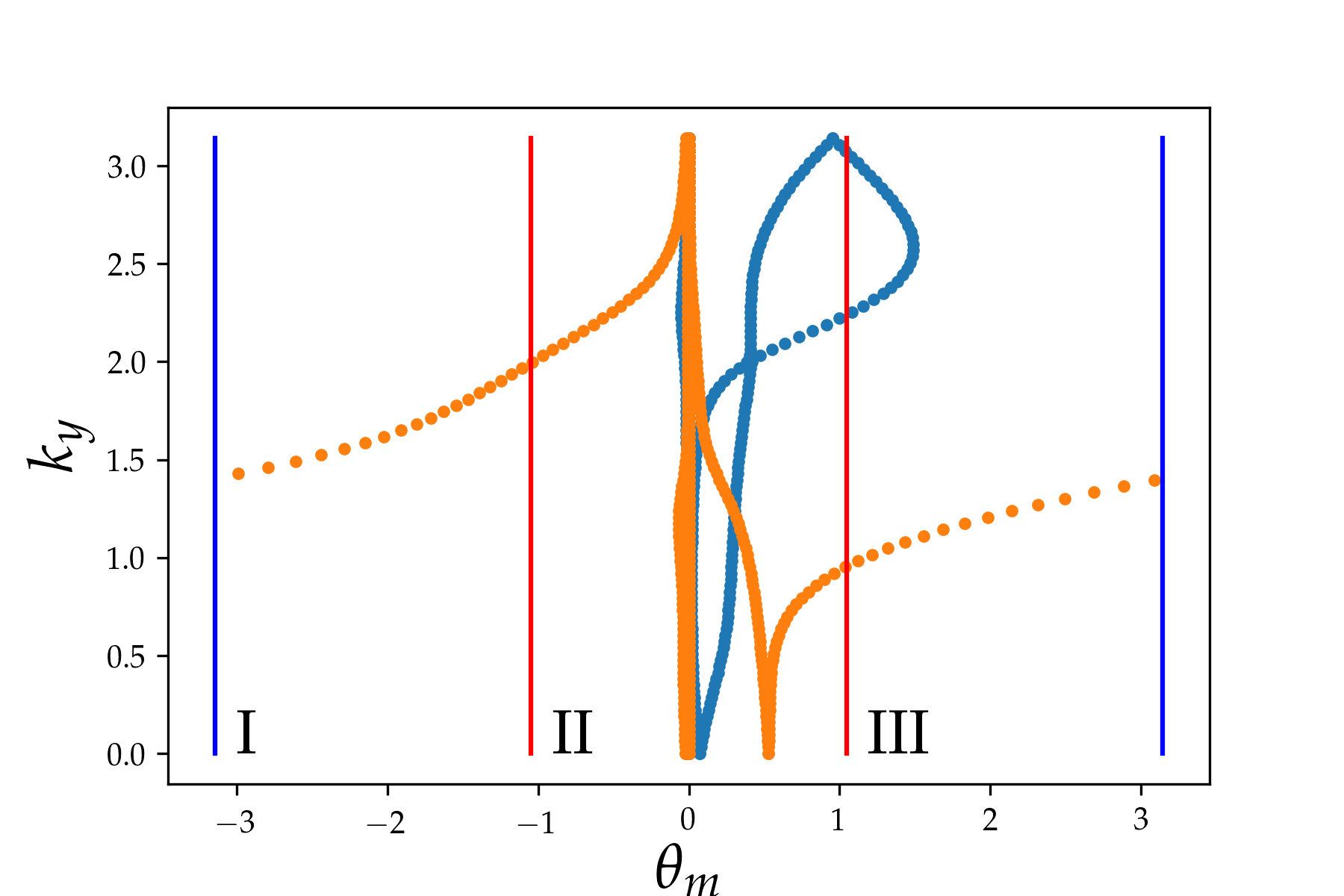 Z2 characterization for three-dimensional multiband Hubbard models
Z2 characterization for three-dimensional multiband Hubbard models
(arXiv:1910.08030, Phys. Rev. Research 2, 013299 (2020))
We introduce three numerical methods for characterizing the topological phases of three-dimensional multiband Hubbard models based on twisted boundary conditions, Wilson loops, as well as the local topological marker. We focus on the half-filled, three-dimensional time-reversal-invariant Hofstadter model with finite spin-orbit coupling. Besides the weak and strong topological insulator phases we find a nodal line semimetal in the parameter regime between the two three-dimensional topological insulator phases. Using dynamical mean-field theory combined with the topological Hamiltonian approach we find stabilization of these three-dimensional topological states due to the Hubbard interaction. We study surface states which exhibit an asymmetry between left and right surfaces originating from the broken parity symmetry of the system. Our results set the stage for further research on inhomogeneous three-dimensional topological systems, proximity effects, topological Mott insulators, nontrivially linked nodal line semimetals, and circuit-based quantum simulators.
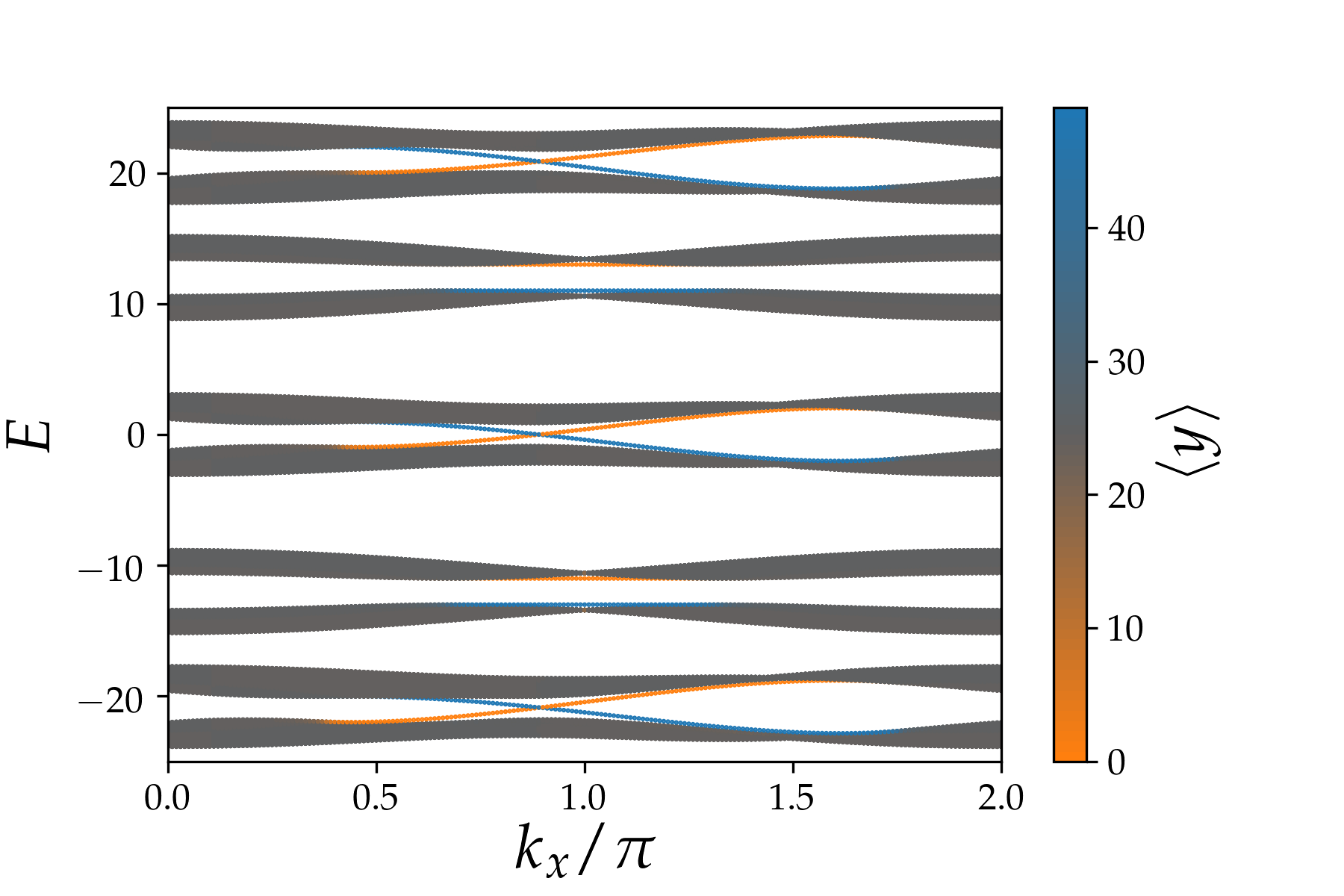 Bulk topological proximity effect in multilayer systems
Bulk topological proximity effect in multilayer systems
(arXiv:1910.05197, Phys. Rev. B 102, 075403 (2020))
We investigate the bulk topological proximity effect in multilayer lattice systems. We show that one can introduce topological properties into a system composed of multiple trivial layers by coupling to a single nontrivial layer described by the Haldane model. This phenomenon depends not only on the number of layers but also on their arrangement, which can lead to the emergence of dark states in multilayer systems. The response of a trivial system to the proximity of a topological insulator appears to be highly nonlocal, in contrast to the proximity effect observed in context of superconductivity. We also find a range of parameters where our system is semimetallic with features similar to the ones observed in three-dimensional topological states. This is promising from the perspective of bridging two- and three-dimensional topologically protected states of matter.
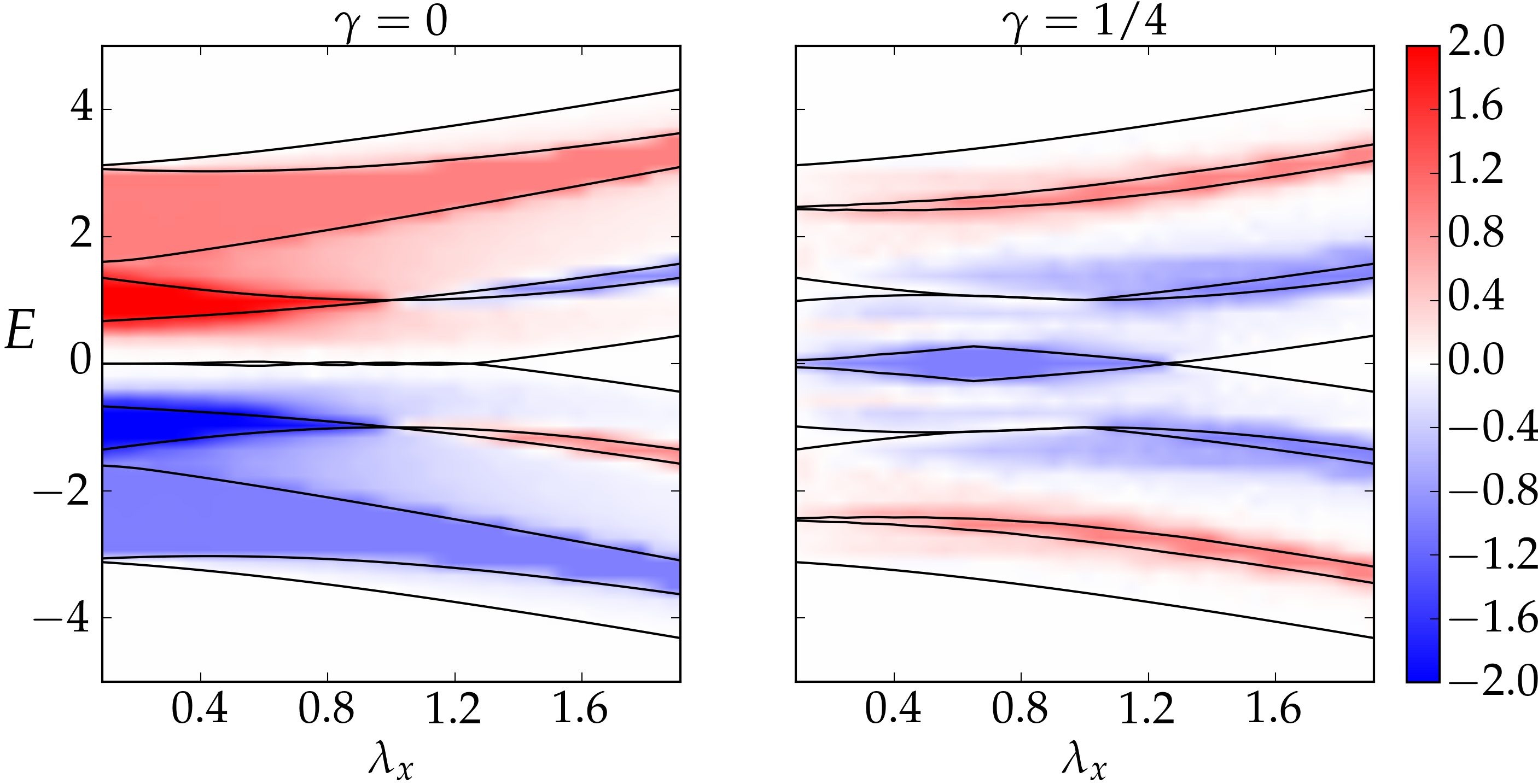 Local Chern marker of smoothly confined Hofstadter fermions
Local Chern marker of smoothly confined Hofstadter fermions
(arXiv:1906.11164, Phys. Rev. A 101, 0636306 (2020))
The engineering of topological non-trivial states of matter, using cold atoms, has made great progress in the last decade. Driven by experimental successes, it has become of major interest in the cold atom community. In this work we investigate the time-reversal invariant Hofstadter model with an additional confining potential. By calculating a local spin Chern marker we find that topologically non-trivial phases can be observed in all considered trap geometries. This holds also for spin-orbit coupled fermions, where the model exhibits a quantum spin Hall regime at half filling. Using dynamical mean-field theory, we find that interactions compete against the confining potential and induce a topological phase transition depending on the filling of the system. Strong interactions furthermore yield a magnetic edge, which is localized through the interplay of the density distribution and the underlying topological band structure.
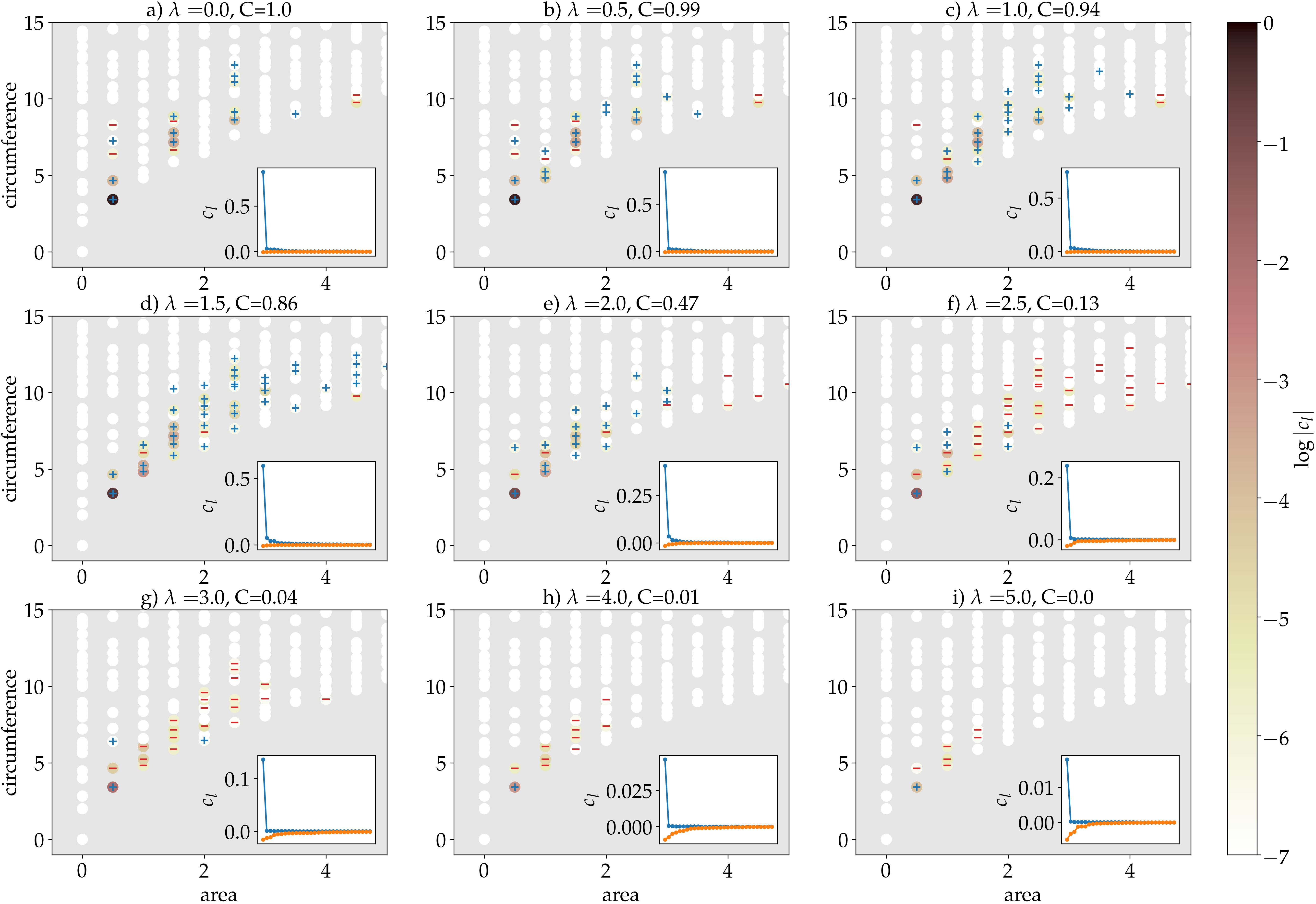 Microscopic characteristics and tomography scheme of the local Chern marker
Microscopic characteristics and tomography scheme of the local Chern marker
(arXiv:1904.03091, Phys. Rev. A 100, 023610 (2019))
The concept of the local Chern marker has gained a lot of attention especially in the field of ultracold quantum gases in optical lattices and artificial gauge fields. We investigate in further detail the microscopic real-space characteristics of the local Chern marker for the two-band Harper-Hofstadter-Hatsugai model and propose a tomographic scheme for the experimental detection of an approximate local Chern marker neglecting higher orders.
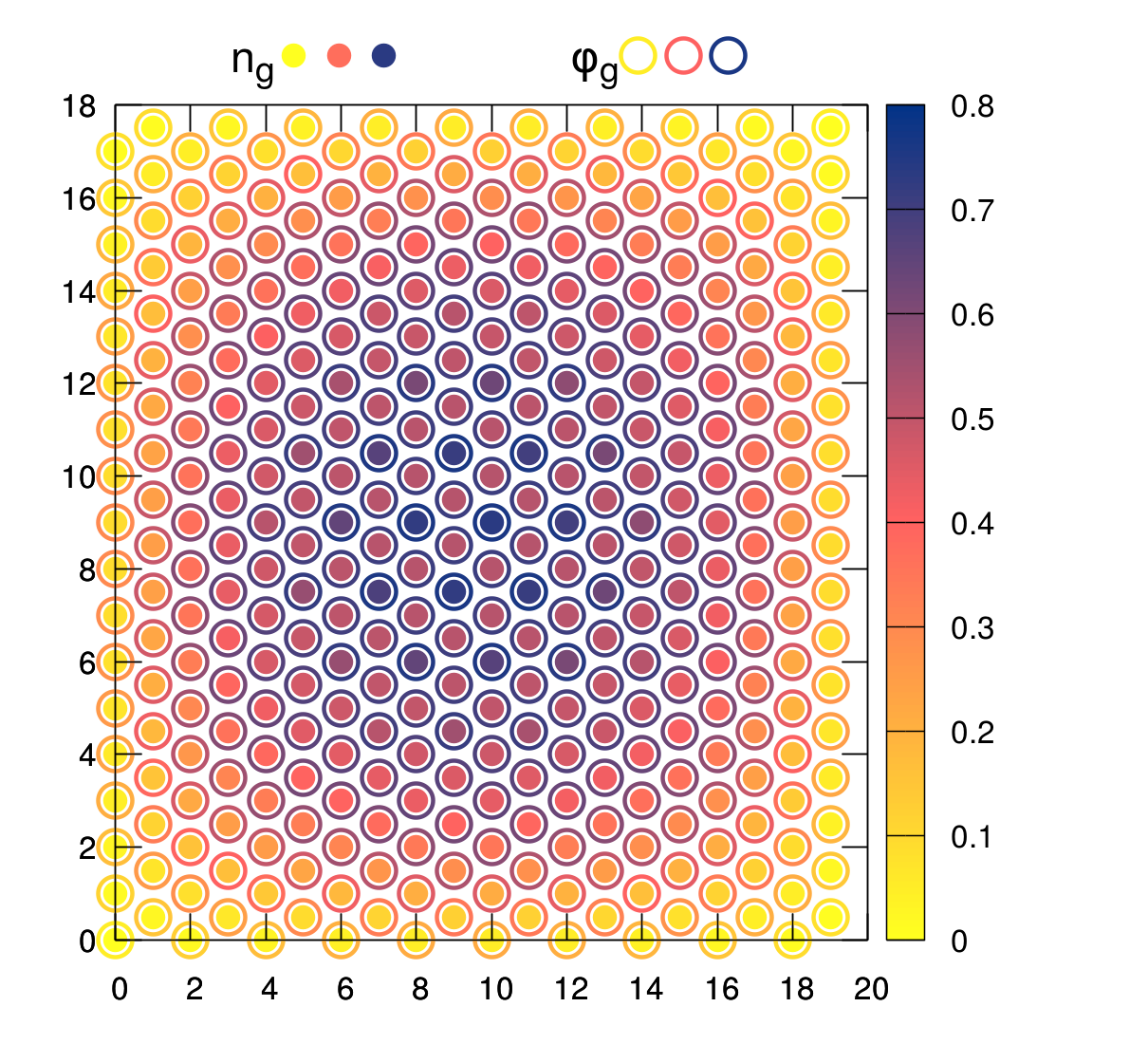 Supersolid phases of Rydberg-excited bosons on a triangular lattice
Supersolid phases of Rydberg-excited bosons on a triangular lattice
(arXiv:1903.01912, Phys. Rev. A 99, 063625 (2019))
Recent experiments with ultracold Rydberg-excited atoms have shown that long-range interactions can give rise to spatially ordered structures. Observation of crystalline phases in a system with Rydberg atoms loaded into an optical lattice seems also within reach. Here we investigate a bosonic model on a triangular lattice suitable for description of such experiments. Numerical simulations based on bosonic dynamical mean-field theory reveal a rich phase diagram with different supersolid phases. Comparison with the results obtained for a square lattice geometry shows qualitatively similar results in a wide range of parameters, however, on a triangular lattice we do not observe the checkerboard supersolid. Moreover, unlike on a square lattice we did not find a phase transition from uniform superfluid to supersolid induced by increase of the hopping amplitude on a triangular lattice. Based on our results we propose an intuitive interpretation of the nature of different supersolid phases. We also propose parameters for the experimental realization.
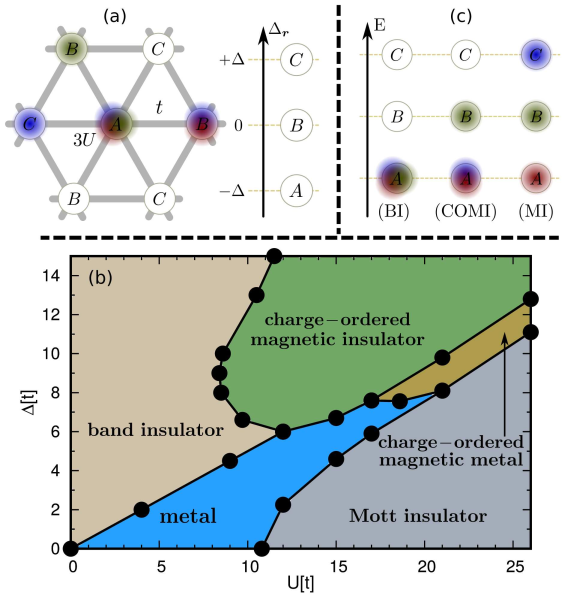 Competing Charge and Magnetic Order in Fermionic Multi-Component Systems
Competing Charge and Magnetic Order in Fermionic Multi-Component Systems
(arXiv:1901.02054, Phys. Rev. B 100, 035133 (2019))
We consider the fermionic SU(3) Hubbard model on the triangular lattice in the presence of a three-sublattice staggered potential which provides the possibility to investigate the competition of charge and magnetic order in three-component systems. We show that depending on the strength of the staggered potential Δ, the Hubbard interaction U destabilizes the band insulator (BI) at small U into the Mott insulator (MI) at large U in three different ways with different intermediate phases. This leads to a rich phase diagram in the U-Δ plane. Our results indicate that multi-component systems show not only exotic states in the Mott regime as has been considered previously, but also interesting competition between charge and magnetic orders.
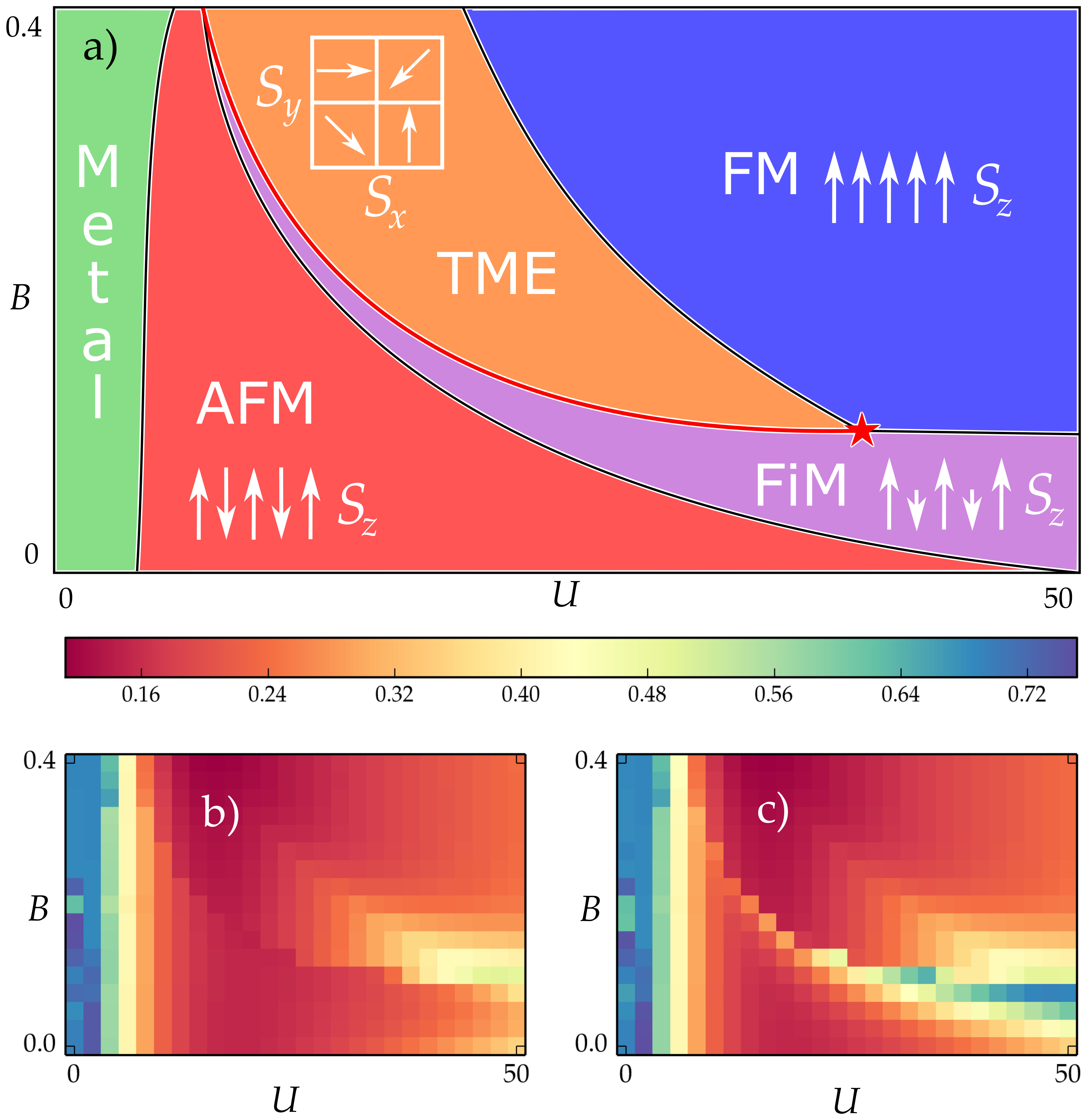 Transverse Magnetization Effect of the Spin-Imbalanced Hofstadter-Hubbard Model
Transverse Magnetization Effect of the Spin-Imbalanced Hofstadter-Hubbard Model
(arXiv:1812.02001, Phys. Rev. A 99, 043628 (2019))
We spin-imbalance the fermionic, time-reversal invariant Hofstadter-Hubbard model through a population difference between two spin states. In the strongly interacting regime, where the system can be described by an effective spin model, we find an exotic spin structure by means of classical Monte-Carlo calculations. Remarkably, this spin structure exhibits a finite transverse net magnetization perpendicular to the magnetization induced by the population imbalance. We further investigate effects of quantum fluctuations within the dynamical mean-field approximation and obtain a rich phase diagram including ferromagnetic, anti-ferromagnetic, and ferrimagnetic phases, where the latter shows strong interaction-induced quantum entanglement.
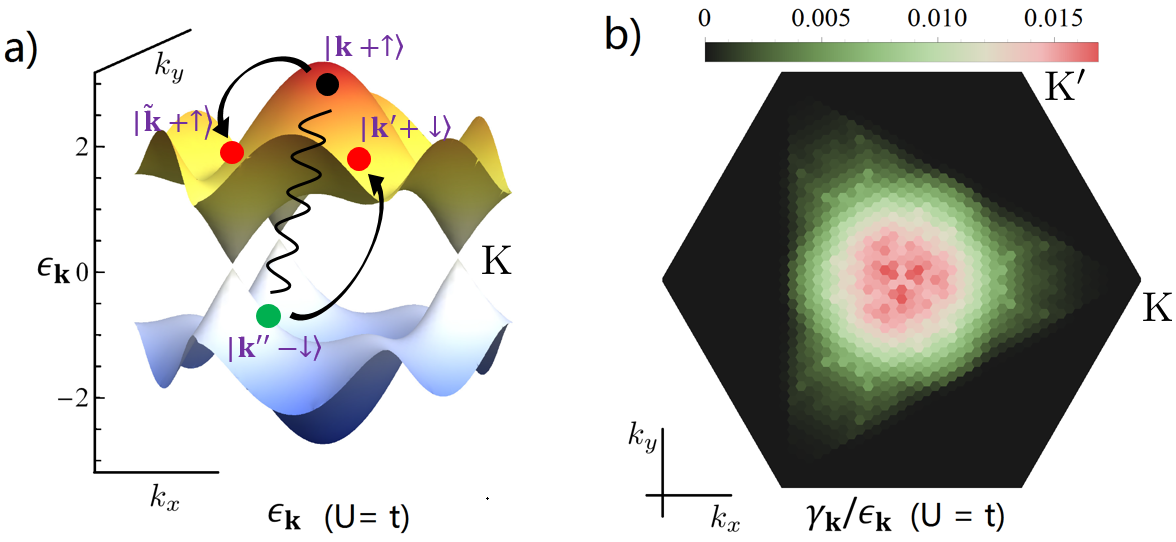 Measuring an interaction-induced topological phase transition via the single-particle density matrix
Measuring an interaction-induced topological phase transition via the single-particle density matrix
(arXiv:1812.01991, Phys. Rev. A 101, 013631 (2020))
Interaction-induced topologically nontrivial phases have been theoretically predicted and need more experimental verification. Cold atom systems with tunable interaction strength provide a flexible platform for studying these effects. Here, we focus on the experimental signature of topological phase and topological phase transition (TPT). Since the topological Hamiltonian carries the information of the topology of the system, we first establish its relation to the single-particle density matrix (SPDM) for interacting two-band systems, and then design a tomography scheme for the SPDM in cold atom experiments. Thus the Berry curvature of the topological Hamiltonian, the Chern number, and the TPT point can be reconstructed from experimental data.
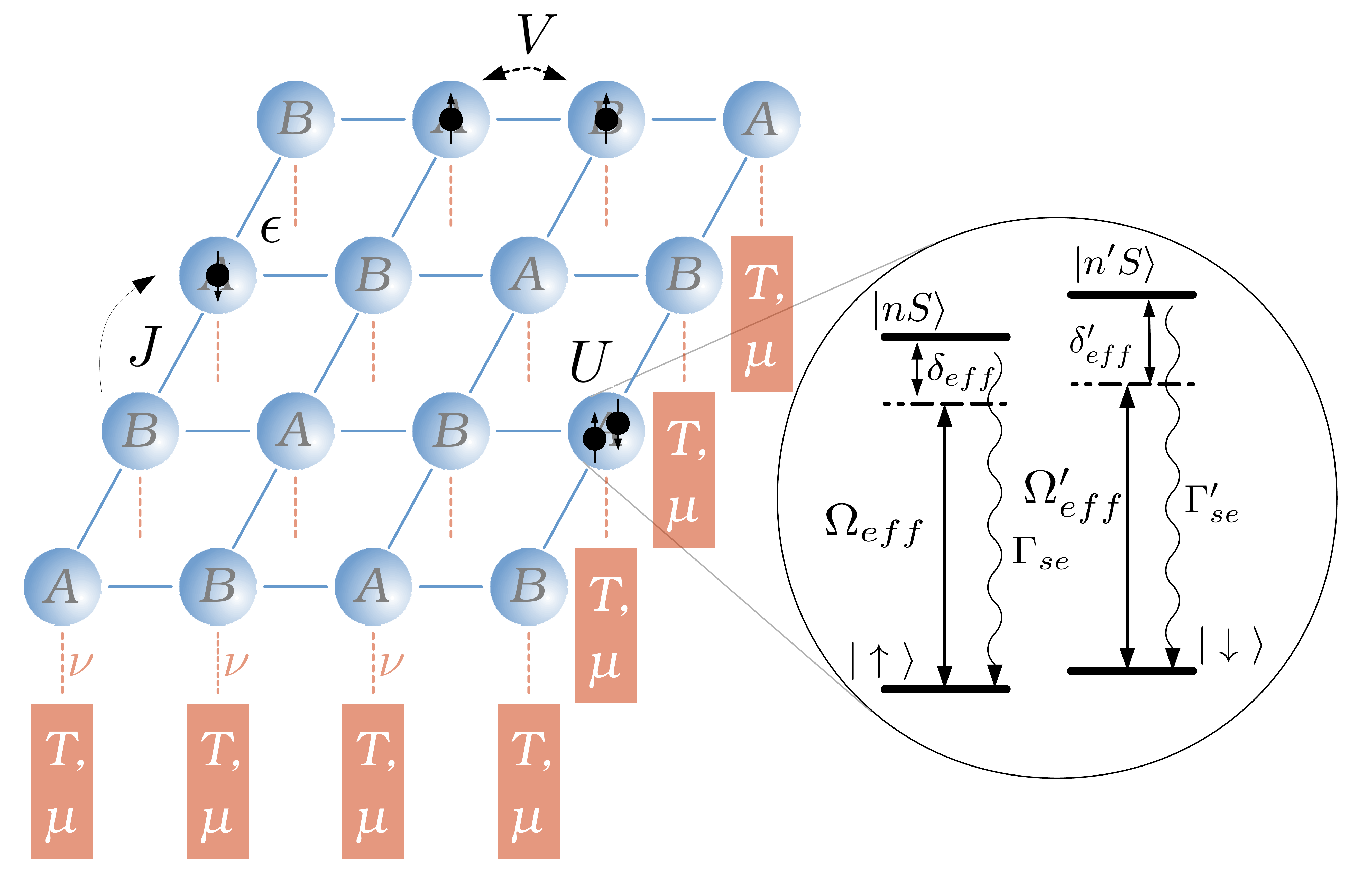 Density-wave steady-state phase of dissipative ultracold fermions with nearest-neighbor interactions
Density-wave steady-state phase of dissipative ultracold fermions with nearest-neighbor interactions
(arXiv:1811.07369, Phys. Rev. B 99, 115125 (2019))
In this work we investigate the effect of local dissipation on the presence of density-wave ordering in spinful fermions with both local and nearest-neighbor interactions as described by the extended Hubbard model. We find density-wave order to be robust against decoherence effects up to a critical point where the system becomes homogeneous with no spatial ordering. Our results will be relevant for future cold-atom experiments using fermions with non-local interactions arising from the dressing by highly-excited Rydberg states, which have finite lifetimes due to spontaneous emission processes.
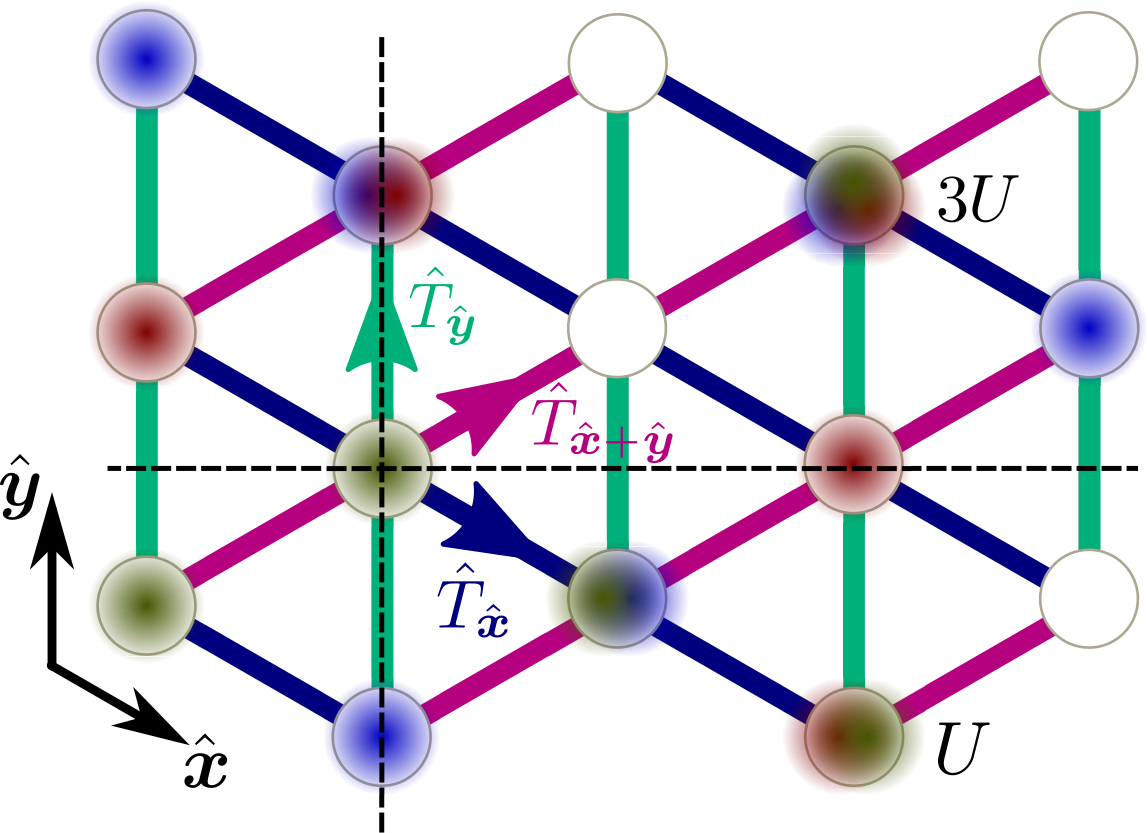 Artificial SU(3) Spin-Orbit Coupling and Exotic Mott Insulators
Artificial SU(3) Spin-Orbit Coupling and Exotic Mott Insulators
(arXiv:1809.05704, Phys. Rev. B 98, 245131 (2018))
Motivated by recent progress in the realization of artificial gauge fields and SU(N) Mott insulators using alkaline-earth-like atoms in optical lattices, we study the effect of spin-orbit coupling and onsite Hubbard interaction U on SU(3) fermionic systems using an unbiased real-space dynamical mean-field theory (DMFT) approach. We investigate the behavior of the local magnetization, double occupancies, and the triple occupancy versus the Hubbard interaction across the metal to Mott insulator transition. We map out the magnetic phase diagram in the large-U limit and show that the spin-orbit coupling can stabilize long-range orders such as ferromagnet, spiral, and stripes with different orientations in SU(3) Mott insulators.
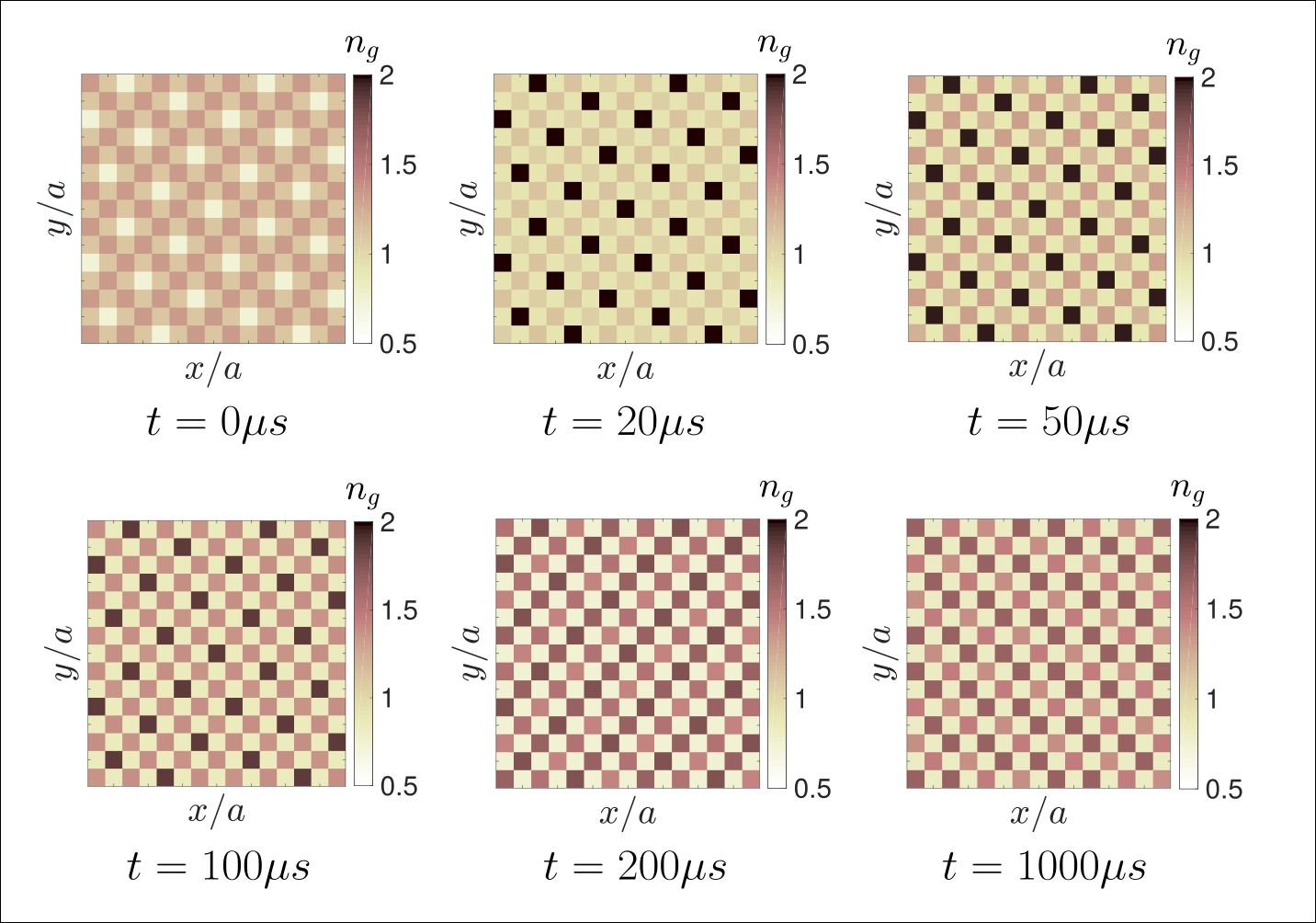 Decay-dephasing-induced steady states in bosonic Rydberg-excited quantum gases in an optical lattice
Decay-dephasing-induced steady states in bosonic Rydberg-excited quantum gases in an optical lattice
(arXiv:1806.08588, Phys. Rev. A 99, 033602 (2019))
We investigate the possibility of realizing supersolid quantum phases in bosonic Rydberg-excited quantum lattice gases in the presence of non-unitary processes, by simulating the dynamical evolution starting from initial preparation in non-dissipative equilibrium states. Within Gutzwiller theory, we first analyze the many-body ground-state of a bosonic Rydberg-excited quantum gas in a two dimensional optical lattice for variable atomic hopping rates and Rabi detunings. Furthermore, we perform time evolution of different supersolid phases using the Lindblad-master equation. With the inclusion of two different non-unitary processes, namely spontaneous decay from a Rydberg state to the ground state and dephasing of the addressed Rydberg state, we study the effect of non-unitary processes on those quantum phases and observe long-lived states in the presence of decay and dephasing. We find that long-lived supersolid quantum phases are observable within a range of realistic decay and dephasing rates, while high rates cause any initial configuration to homogenize quickly, preventing possible supersolid formation.
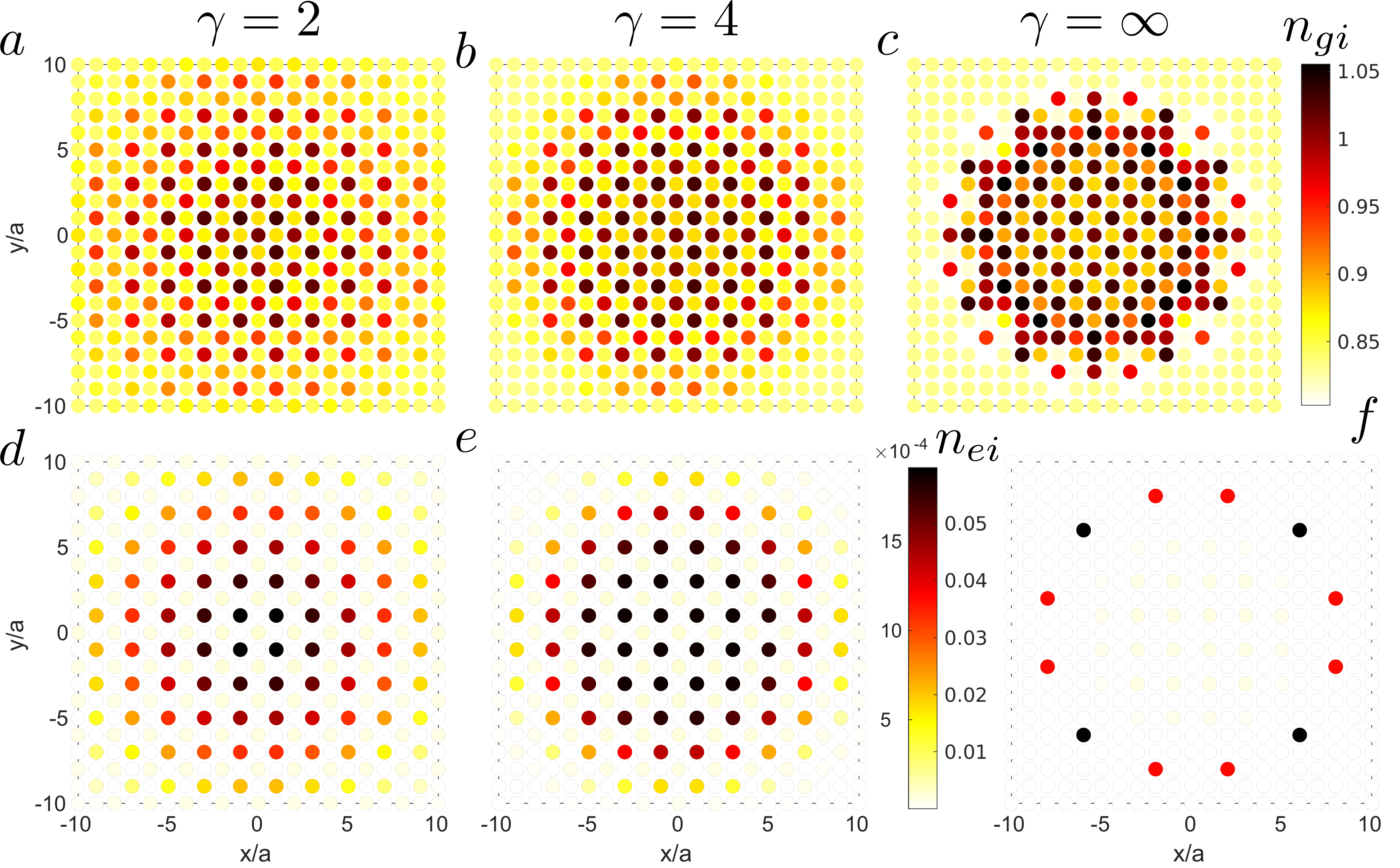 Quasiparticle spectra of supersolid lattice gases at near-resonant Rydberg-dressing
Quasiparticle spectra of supersolid lattice gases at near-resonant Rydberg-dressing
(arXiv:1806.05911, Phys. Rev. A 98, 063635 (2018))
One of the major challenges in realizing a strongly interacting lattice gas using Rydberg states is the occurrence of avalanche loss processes. As these are directly proportional to the total Rydberg fraction, the commonly suggested solution is using far off-resonantly excited Rydberg states. We instead propose the realization of a correlated bosonic lattice gas at near-resonant excitation, where the total Rydberg fraction in the bulk is low due to the strong, interaction-driven effective detuning. Using real-space dynamical mean-field theory we show that its reduced effect at the boundary of a system can easily be compensated by considering a tailored beam-waist of the driving Rabi-laser. In this geometry we discuss the spectral properties at the crossover between the supersolid and the superfluid state and present the momentum resolved spectral properties of the supersolid bulk. The latter results are obtained within an extended quasiparticle method which also yields a correction of the mean-field phase transition.
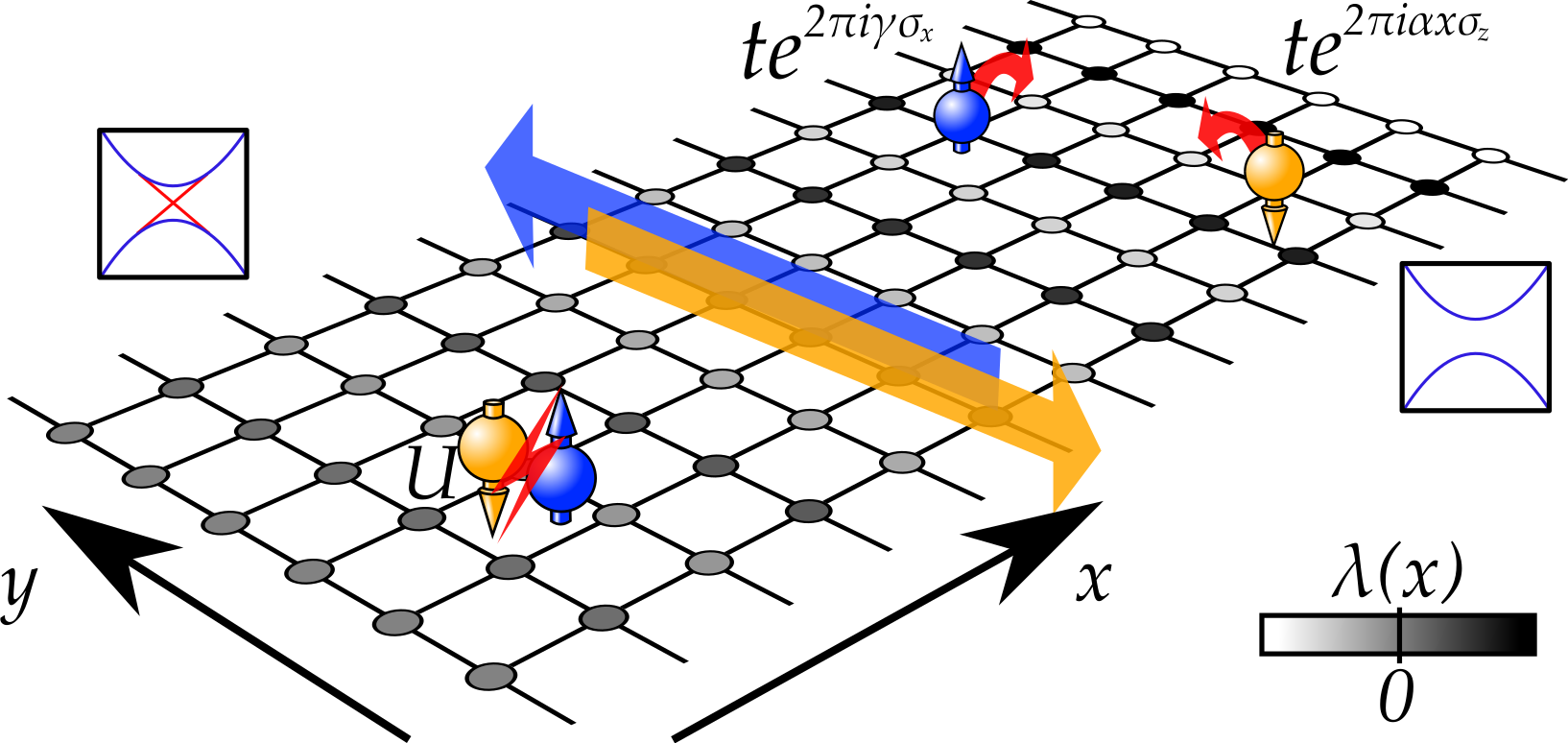 Interacting Hofstadter Interface
Interacting Hofstadter Interface
(arXiv:1806.01598, Phys. Rev. Lett. 122, 010406 (2019), public release)
Two-dimensional topological insulators possess conducting edge states at their boundary while being insulating in the bulk. The detection of edge states remains an open question in ultracold atom setups. We propose a configuration to implement a topological interface within the experimentally realizable time-reversal invariant Hofstadter model which gives rise to a topological phase boundary at the center of the system, and investigate the influence of two-body interactions on the interface in a fermionic system. The interface can in principle be probed via the spatially resolved compressibility of the system by using a quantum gas microscope. Furthermore, we distinguish the phases through their Hall response and compute a local spin Chern marker which proves the phase separation of two distinct topological many-body phases. The bulk-boundary correspondence for the interacting system is confirmed by computing the edge state spectra at the interface.
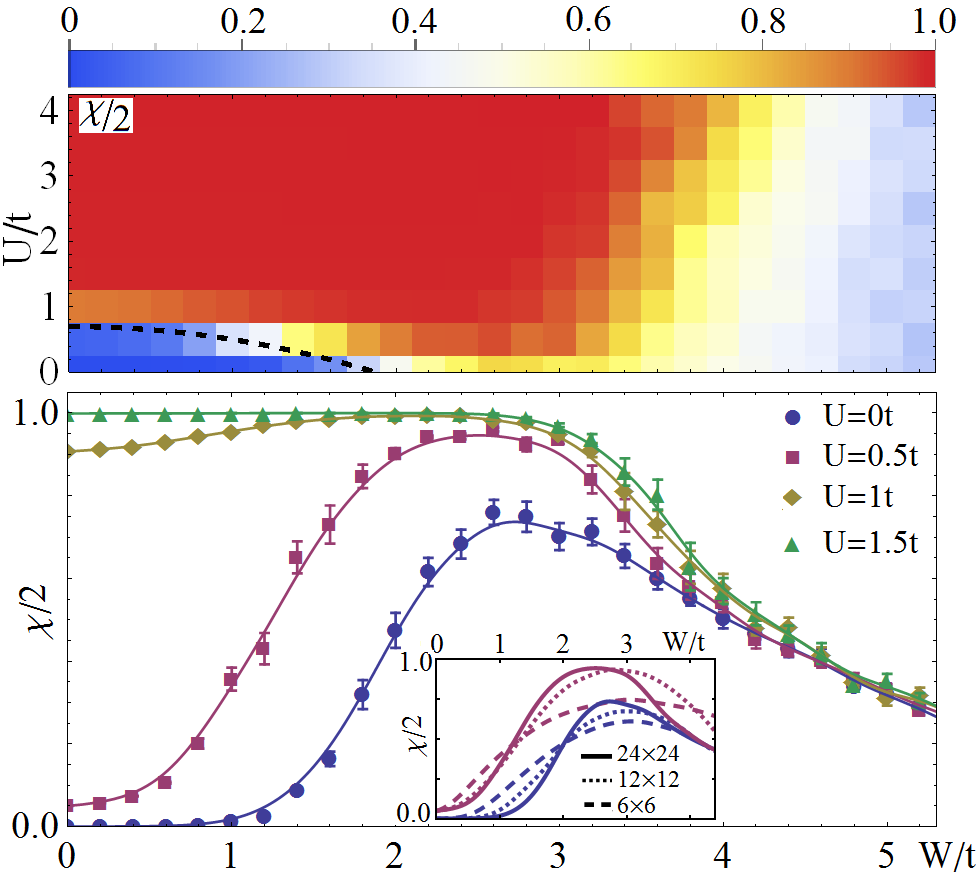 Interaction-enhanced integer quantum Hall effect in disordered systems
Interaction-enhanced integer quantum Hall effect in disordered systems
(arXiv:1805.10491, Phys. Rev. B 99, 125138 (2019))
We study transport properties and topological phase transition in two-dimensional interacting disordered systems. Within dynamical mean-field theory, we derive the Hall conductance, which is quantized and serves as a topological invariant for insulators, even when the energy gap is closed by localized states. In the spinful Harper-Hofstadter-Hatsugai model, in the trivial insulator regime, we find that the repulsive on-site interaction can assist weak disorder to induce the integer quantum Hall effect, while in the topologically non-trivial regime, it impedes Anderson localization. Generally, the interaction broadens the regime of the topological phase in the disordered system.
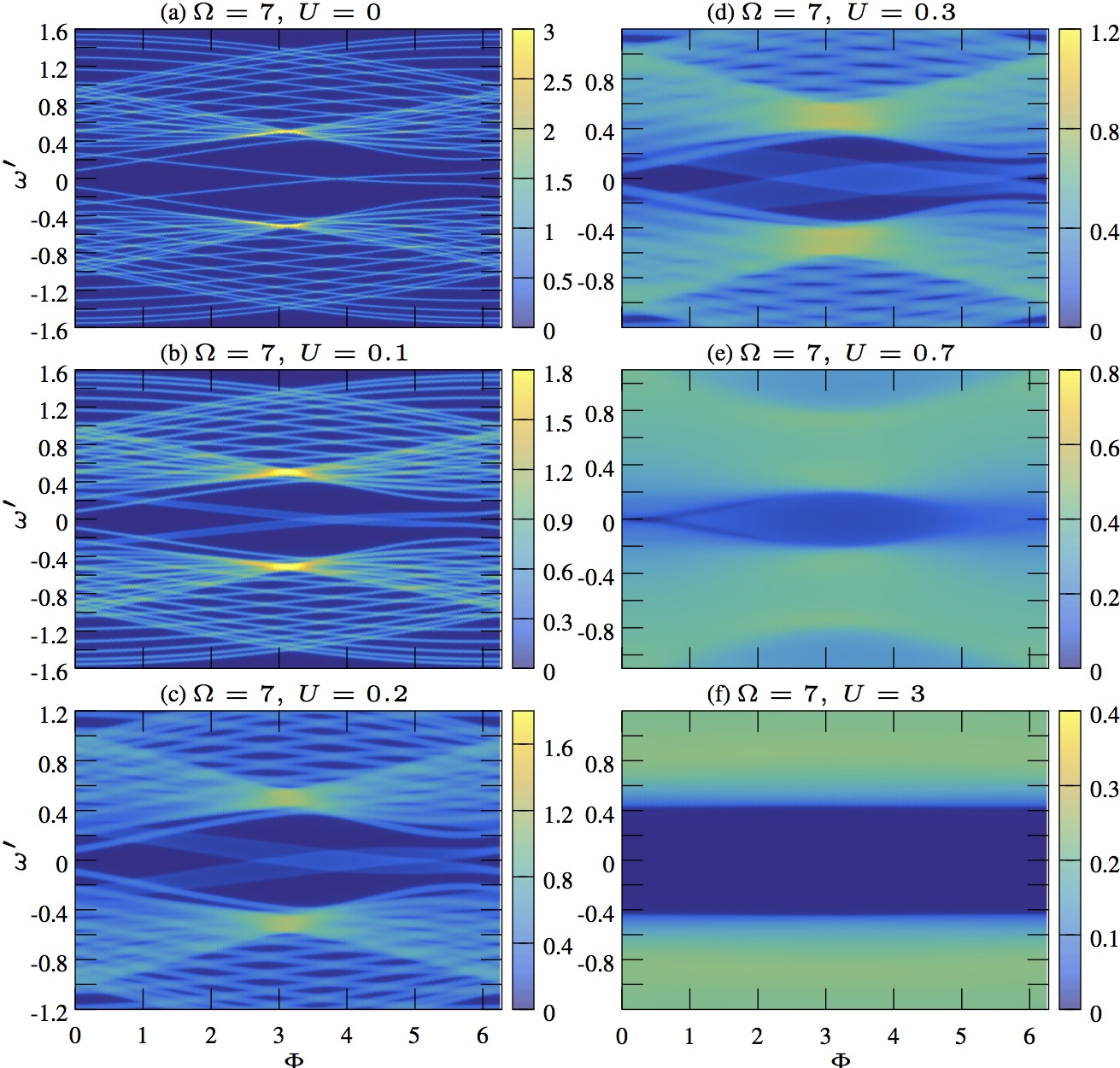 Charge density wave and charge pump of interacting fermions in circularly shaken hexagonal optical lattices
Charge density wave and charge pump of interacting fermions in circularly shaken hexagonal optical lattices
(arXiv:1804.03200, Phys. Rev. A 98, 033601 (2018))
We analyze strong correlation effects and topological properties of interacting fermions with a Falicov-Kimball type interaction in circularly shaken hexagonal optical lattices, which can be effectively described by the Haldane-Falicov-Kimball model, using the real-space Floquet dynamical mean-field theory (DMFT). The Haldane model, a paradigmatic model of the Chern insulator, is experimentally relevant, because it has been realized using circularly shaken hexagonal optical lattices. We show that in the presence of staggering a charge density wave emerges, which is affected by interactions and resonant tunneling. We demonstrate that interactions smear out the edge states by introducing a finite life time of quasiparticles. Even though a general method for calculating the topological invariant of a nonequilibrium steady state is lacking, we extract the topological invariant using a Laughlin charge pump set-up. We find and attribute to the dissipations into the bath connected to every lattice site, which is intrinsic to real-space Floquet DMFT methods, that the pumped charge is not an integer even for the non-interacting case at very low reservoir temperatures. Furthermore, using the rate equation based on the Floquet-Born-Markov approximation, we calculate the charge pump from the rate equations for the non-interacting case to identify the role of the spectral properties of the bath. Starting from this approach we propose an experimental protocol for measuring quantized charge pumping.
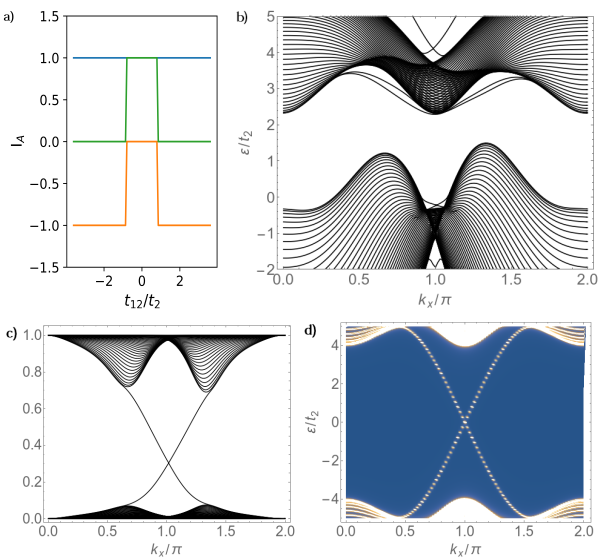 Topological invariant for two-dimensional open systems
Topological invariant for two-dimensional open systems
(arXiv:1710.03119, Phys. Rev. B 97, 195434(2018))
We study the topology of 2D open systems in terms of the Green's function. The Ishikawa-Matsuyama formula for the integer topological invariant is applied in open systems and the equivalent descriptions through topological Hamiltonian and Berry curvature are developed separately. The invariant is well-defined iff all of the eigenvalues of the Green's function for imaginary frequency are finite nonzero numbers. Meanwhile, we define another topological invariant via the single particle density matrix, which works for general gapped systems and is equivalent to the former for the case of weak coupling to an environment. We also discuss two applications. For time-reversal invariant insulators, we explain the relation between the invariant for each spin-subsystem and the Z2 index of the full system. As a second application, we consider the interference effect when an ordinary insulator is coupled to a topological insulator. The bulk-boundary correspondence of the open system shows new features.
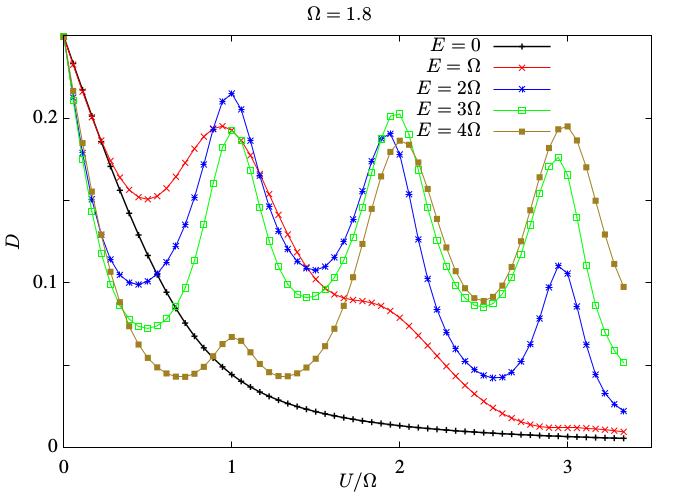 Nonequilibrium Steady States and Resonant Tunneling in Time-Periodically Driven Systems with Interactions
Nonequilibrium Steady States and Resonant Tunneling in Time-Periodically Driven Systems with Interactions
(arXiv:1709.03021, Phys. Rev. B 97, 125115(2018))
Time-periodically driven systems are a versatile toolbox for realizing interesting effective Hamiltonians. Heating, caused by excitations to high-energy states, is a challenge for experiments. While most setups address the relatively weakly-interacting regime so far, it is of general interest to study heating in strongly correlated systems. Using Floquet dynamical mean-field theory, we study non-equilibrium steady states (NESS) in the Falicov-Kimball model, with time-periodically driven kinetic energy or interaction. We systematically investigate the non-thermalized properties of the NESS. For a driven kinetic energy, we show that resonant tunneling, where the interaction is an integer multiple of the driving frequency, plays an important role in the heating. In the strongly correlated regime, we show that this can be well understood using Fermi's Golden rule and the Schrieffer-Wolff transformation for a time-periodically driven system. We furthermore demonstrate that resonant tunneling can be used to control the population of Floquet states to achieve "photo-doping". For driven interactions, we find that the double occupancy is strongly modulated.
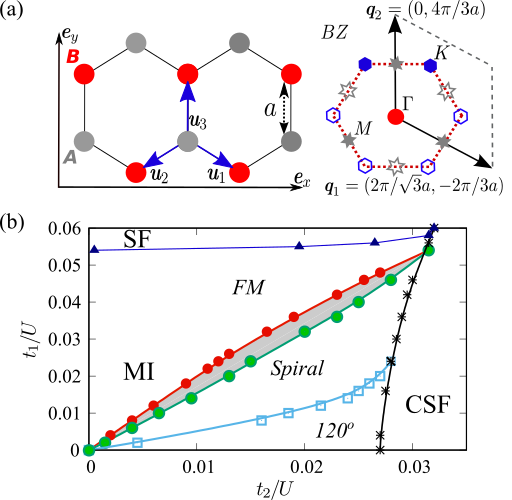 Emergent Chiral Spin State in the Mott Phase of a Bosonic Kane-Mele-Hubbard Model
Emergent Chiral Spin State in the Mott Phase of a Bosonic Kane-Mele-Hubbard Model
(arXiv:1707.07037, Phys. Rev. Lett. 120, 157201(2018))
Recently, the frustrated XY model for spins-1/2 on the honeycomb lattice has attracted a lot of attention in relation with the possibility to realize a chiral spin liquid state. This model is relevant to the physics of some quantum magnets. Using the flexibility of ultra-cold atoms setups, we propose an alternative way to realize this model through the Mott regime of the bosonic Kane-Mele-Hubbard model. The phase diagram of this model is derived using the bosonic dynamical mean-field theory. Focussing on the Mott phase, we investigate its magnetic and topological properties as a function of frustration using exact diagonalization and bosonic dynamical mean-field theory. We do find an emergent chiral spin state in the intermediate frustration regime. This gapped phase displays a chiral order, breaking time-reversal and parity symmetry, but its Chern number is zero.
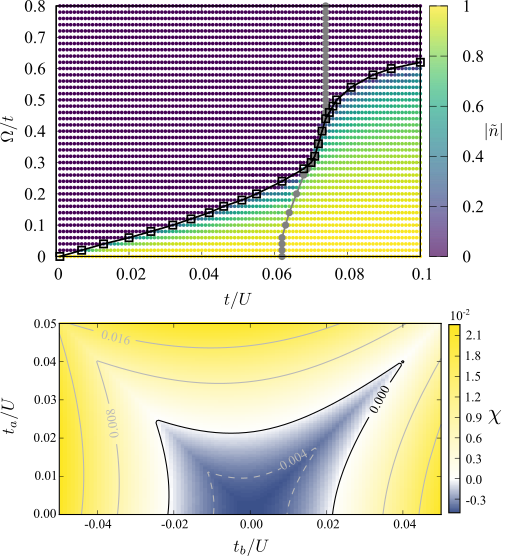 Phase transitions of the coherently coupled two-component Bose gas in a square optical lattice
Phase transitions of the coherently coupled two-component Bose gas in a square optical lattice
(arXiv:1705.02833, Phys. Rev. A 96, 063623(2017))
We investigate properties of an ultracold, two-component bosonic gas in a square optical lattice at unit filling. In addition to density-density interactions, the atoms are subject to coherent light-matter interactions that couple different internal states. We examine the influence of this coherent coupling on the system and its quantum phases by using Gutzwiller mean field theory as well as bosonic dynamical mean field theory. We find that the interplay of strong inter-species repulsion and coherent coupling affects the Mott insulator to superfluid transition and shifts the tip of the Mott lobe toward higher values of the tunneling amplitude. In the strongly interacting Mott regime, the resulting Bose-Hubbard model can be mapped onto an effective spin Hamiltonian that offers additional insights into the observed phenomena.
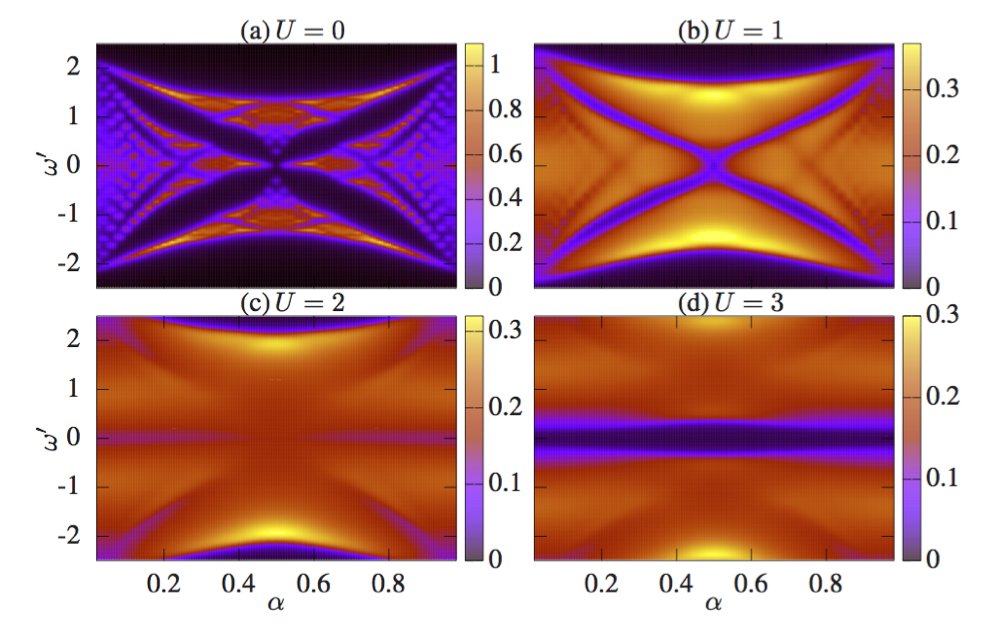 Spectral functions of a time-periodically driven Falicov-Kimball model: real-space Floquet DMFT study
Spectral functions of a time-periodically driven Falicov-Kimball model: real-space Floquet DMFT study
(arXiv:1704.03250, Phys. Rev. B 96, 075134(2017))
We present a systematic study of spectral functions of a time-periodically driven Falicov-Kimball Hamiltonian. In the high-frequency limit, this system can be effectively described as a Harper-Hofstadter-Falicov-Kimball model. Using real-space Floquet dynamical mean-field theory (DMFT), we take into account interaction effects and contributions from higher Floquet bands in a non-perturbative way. Our calculations show a high degree of similarity between the interacting driven system and its effective static counterpart with respect to spectral properties. However, as also illustrated by our results, one should bear in mind that Floquet DMFT describes a non-equilibrium steady state (NESS), while an effective static Hamiltonian describes an equilibrium state. We further demonstrate the possibility of using real-space Floquet DMFT to study edge states on a cylinder geometry.
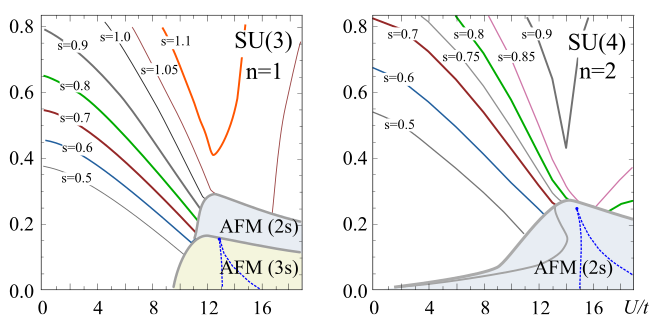 Breaking of SU(4) symmetry and interplay between strongly-correlated phases in the Hubbard model
Breaking of SU(4) symmetry and interplay between strongly-correlated phases in the Hubbard model
(arXiv:1612.06258, Phys. Rev. B 95, 125108(2017))
We study thermodynamic properties of four-component fermionic mixtures described by the Hubbard model using the dynamical mean-field theory approach. Special attention is given to the system with SU(4)-symmetric interactions at half filling, where we analyze equilibrium many-body phases and their coexistence regions at nonzero temperature for the case of simple cubic lattice geometry. We also determine the evolution of observables in low-temperature phases while lowering the symmetry of the Hamiltonian towards the two-band Hubbard model. This is achieved by varying interflavor interactions or by introducing the spin-flip term (Hund's coupling). By calculating the entropy for different symmetries of the model we determine the optimal regimes for approaching the studied phases in experiments with ultracold alkali and alkaline-earth-like atoms in optical lattices.
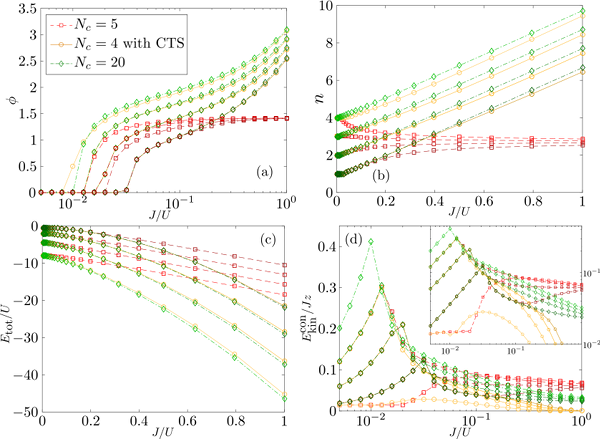 The infinite occupation number basis of bosons - solving a numerical challenge
The infinite occupation number basis of bosons - solving a numerical challenge
(arXiv:1611.10185, Phys. Rev. B 95, 224516(2017))
In any bosonic lattice system, which is not dominated by local interactions and thus "frozen" in a Mott-type state, numerical methods have to cope with the infinite size of the corresponding Hilbert space even for finite lattice sizes. While it is common practice to restrict the local occupation number basis to Nc lowest occupied states, the presence of a finite condensate fraction requires the complete number basis for an exact representation of the many-body ground state. In this work we present a novel truncation scheme to account for contributions from higher number states. By simply adding a single \textit{coherent-tail} state to this common truncation, we demonstrate increased numerical accuracy and the possible increase in numerical efficiency of this method for the Gutzwiller variational wave function and within dynamical mean-field theory.
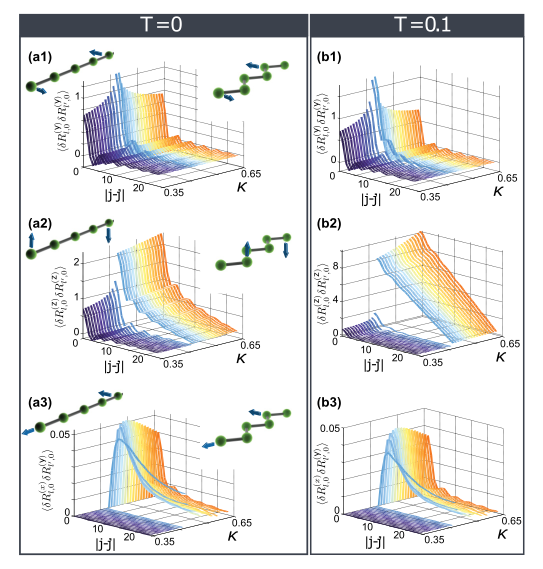 Operator-based derivation of phonon modes and characterization of correlations for trapped ions at zero and finite temperaturel
Operator-based derivation of phonon modes and characterization of correlations for trapped ions at zero and finite temperaturel
(arXiv:1608.07235, Phys. Rev. B 94, 214305(2016))
We present a self-contained operator-based approach to derive the spectrum of trapped ions. This approach provides the complete normal form of the low-energy quadratic Hamiltonian in terms of bosonic phonons, as well as an effective free-particle degree of freedom for each spontaneously broken spatial symmetry. We demonstrate how this formalism can directly be used to characterize an ion chain both in the linear and the zigzag regimes. In particular, we compute, both for the ground state and finite temperature states, spatial correlations, heat capacity, and dynamical susceptibility. Last, for the ground state, which has quantum correlations, we analyze the amount of energy reduction compared to an uncorrelated state with minimum energy, thus highlighting how the system can lower its energy by correlations.
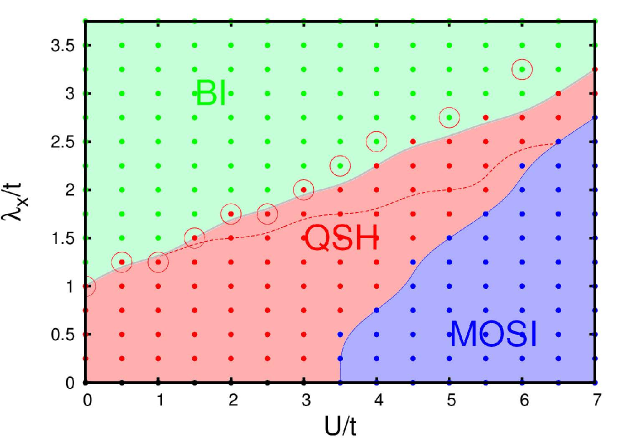 Interaction-Induced Topological and Magnetic Phases in the Hofstadter-Hubbard Model
Interaction-Induced Topological and Magnetic Phases in the Hofstadter-Hubbard Model
(arXiv:1606.09161, Phys. Rev. B 94, 115161(2016))
Interaction effects have been a subject of contemporary interest in topological phases of matter. But in the presence of interactions, the accurate determination of topological invariants in their general form is difficult due to their dependence on multiple integrals containing Green's functions and their derivatives. Here we employ the recently proposed "effective topological Hamiltonian" approach to explore interaction-induced topological phases in the time-reversal-invariant Hofstadter-Hubbard model. Within this approach, the zero-frequency part of the self-energy is sufficient to determine the correct topological invariant. We combine the topological Hamiltonian approach with the local self-energy approximation within Hartree-Fock and dynamical mean field theory (DMFT), and present the resulting phase diagram in the presence of many-body interactions. We investigate the emergence of quantum spin Hall (QSH) states for different interaction strengths by calculating the Z2 invariant. The interplay of strong correlations and a staggered potential also induces magnetic long-range order with an associated first order transition. We present results for the staggered magnetisation (ms), staggered occupancy (ns) and double occupancy across the transition.