Fortgeschrittene Optimierung und inverse Probleme:

Regularisierung inverser Probleme

Prof. Dr. Bastian von Harrach

Dr. Sarah Eberle

Sommersemester 2021

 

Aktuelles

  • Die Modulprüfung findet in Form mündlicher Prüfungen am 13. und 15.07.2021 jeweils Nachmittags statt. Bitte melden Sie sich bis zum 31.05.2021 bei Frau Gharadaghy (gharadaghy@math.uni-frankfurt.de) an.
  • Aktuelle Informationen der Universität zum Umgang mit dem Corona-Risiko finden Sie hier. Die Vorlesungszeit des Sommersemesters beginnt am 12.04.2021.
  • Die Vorlesung findet bis auf Weiteres in digitaler Form ohne Präsenz statt. Es werden wöchentlich (jeweils Mittwochs bis 14 Uhr) beginnend am 14.04.2021 Vorlesungsvideos bereit gestellt.
  • Bitte melden Sie sich zur digitalen Übung bis zum 16.04.2021 per E-Mail an eberle@math.uni-frankfurt.de an. Nutzen Sie dazu Ihre studentische E-Mail-Adresse und geben Sie dabei auch Ihre Matrikelnummer an.
  • Unter Materialien erscheinen im zweiwöchigen Rhythmus (jeweils Mittwochs bis 14 Uhr) beginnend am 14.04.2021 Übungsblätter. Der Abgabemodus wird unter dem Punkt Übungen erläutert. Die Lösungsvideos zu den Übungsblättern werden Dienstags bis 10 Uhr veröffentlicht. Die online-Fragestunde findet im zweiwöchigen Rhythmus jeweils Dienstags von 14-16 Uhr via Zoom statt. Genauere Informationen erhalten Sie per Mail.
  • Für jedwede Fragen wenden Sie sich bitte an die Übungsleiterin.

 

Inhalt und Ziele

Viele Vorgänge in den Natur- und Wirtschaftwissenschaften führen auf sogenannte schlechtgestellte inverse Probleme (Wikipedia-Link). Schlechtgestelltheit bedeutet dabei, dass die gesuchte Größe nicht stetig von den vorhandenen Daten abhängt. Ein einfaches Beispiel für Schlechtgestelltheit ist die numerische Differentiation: Ist eine Funktion nur bis auf einen gewissen Mess- oder Approximationsfehler genau bekannt, so wird durch ''naives'' Ableiten der Funktion (etwa durch finite Differenzen) ein vorhandener Messfehler massiv verstärkt – bis hin zur völligen Unbrauchbarkeit des Ergebnisses.

   

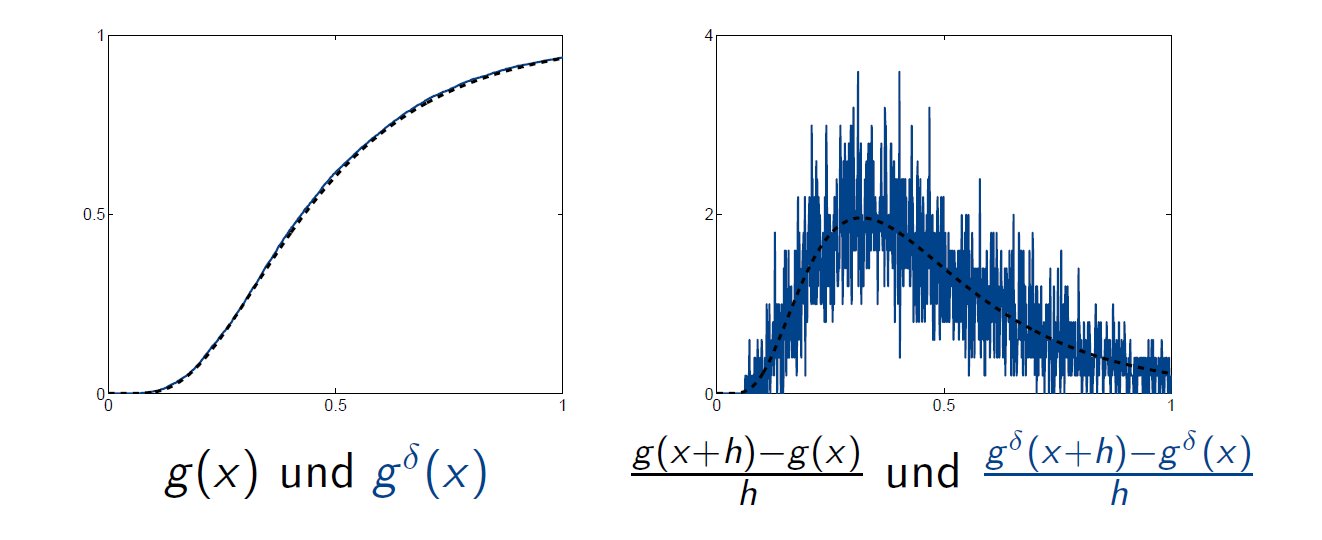Fehlerverstärkung bei numerischer Differentiation

Schlechtgestellte Probleme treten häufig als inverse Probleme zu gutgestellten Problemen auf. So ist etwa die Differentiation das inverse Problem zur gutgestellten Integration, die Messfehler typischerweise reduziert.

An schlechtgestellten Problemen führt in der Praxis oft kein Weg vorbei. Die numerische Differentiation ist z.B. für die Risikobewertung von Finanzderivaten unerlässlich. Typische Quelle schlechtgestellter Probleme sind auch die Parameteridentifikation und neuartige medizinische Tomographiemethoden.

   

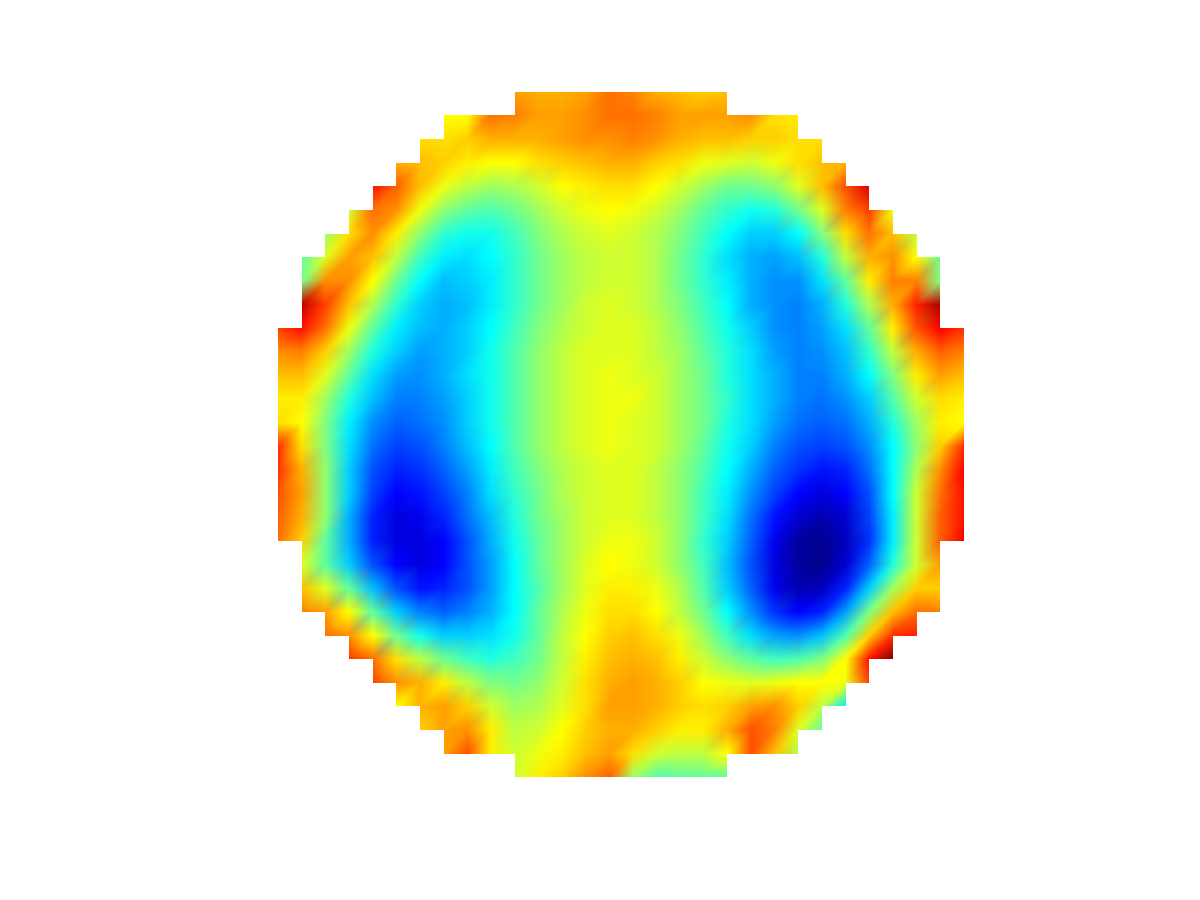Elektrische Impedanz-Tomografie: Schnittbilder der Lunge

In dieser Veranstaltung untersuchen wir, wie inverse Probleme trotz ihrer Schlechtgestelltheit vernünftig (d.h. stabil) gelöst werden können.

Die Veranstaltung richtet sich an Masterstudenten und Bachelorstudenten höheren Semesters. Die benötigten funktionalanalytischen Grundlagen werden in der Vorlesung erarbeitet.

Die Vorlesung ergänzt die Veranstaltung "Optimierung und inverse Probleme" aus dem Wintersemester 2020/21, setzt diese aber nicht voraus und kann auch unabhängig davon gehört werden.

 

Personen

 

Termine (Achtung: Bis auf Weiteres entfallen alle Präsenztermine.)

Vorlesung

Die Vorlesung findet bis auf Weiteres in digitaler Form ohne Präsenz statt. Es werden wöchentlich (jeweils Mittwochs bis 14 Uhr) beginnend am 14.04.2021 Vorlesungsvideos bereit gestellt.

Übungen

  • Bitte melden Sie sich zur digitalen Übung bis zum 16.04.2021 per E-Mail an eberle@math.uni-frankfurt.de an. Nutzen Sie dazu Ihre studentische E-Mail-Adresse und geben Sie dabei auch Ihre Matrikelnummer an.
  • Die Übungsblätter erscheinen im zweiwöchigen Rhythmus (jeweils Mittwochs bis 14 Uhr) beginnend am 14.04.2021.
  • Die Lösungsvideos zu den Übungsblättern werden Dienstags bis 10 Uhr veröffentlicht.
  • Die online-Fragestunde findet im zweiwöchigen Rhythmus jeweils Dienstags von 14-16 Uhr via Zoom statt. Genauere Informationen erhalten Sie per Mail.
    • Zur Abgabe beachten Sie bitte Folgendes:
    • Zu schriftlichen Aufgaben ist eine Ausarbeitung anzufertigen.
    • Zu Programmieraufgaben ist ein kommentierter MATLAB-Quellcode zu schreiben, welcher die entsprechenden Plots generiert.
    • Fügen Sie die eingescannte schriftliche Ausarbeitung sowie den Quellcode und die Plots zu einer einzigen PDF-Datei zusammen und schicken Sie diese an eberle@math.uni-frankfurt.de. Nutzen Sie dazu Ihre studentische E-Mail-Adresse.
    • Zu Votieraufgaben wird keine schriftliche Abgabe verlangt.
    • Die Lösungsvideos finden Sie im HRZ-Videoportal: Kanal Übung Fortgeschrittene Optimierung und inverse Probleme

    Prüfung

    Die Modulprüfung findet in Form mündlicher Prüfungen am 13. und 15.07.2021 jeweils Nachmittags statt. Bitte melden Sie sich bis zum 31.05.2021 bei Frau Gharadaghy (gharadaghy@math.uni-frankfurt.de) an. Teilnahmeberechtigt an der Nachprüfung im Oktober sind ausschließlich nicht erfolgreiche oder aus triftigem Grund entschuldigte Teilnehmerinnen und Teilnehmer der Prüfung. Für die Zulassung zur Modulprüfung sind keine Studienleistungen erforderlich. Wir empfehlen jedoch die Modulprüfung nur dann abzulegen, wenn Sie in den Übungen 50% der Punkte in schriftlichen Aufgaben und Programmieraufgaben erreicht haben. Aktuelle Informationen der Universität zum Umgang mit dem Corona-Risiko finden Sie hier.

     

    Materialien

    Vorlesung

    • Vorlesungsskript (vorläufig, wird ggf. während der Vorlesung korrigiert und ergänzt)

    Übungsblätter

     

    Literatur

    • Andreas Rieder: Keine Probleme mit inversen Problemen. Vieweg, Wiesbaden, 2003

     

    Modulzuordnung