12
Fachbereich
Institut für Mathematik
Toggle navigation EN

Fortgeschrittene Optimierung und inverse Probleme (WS2425)

Aktuelles

  • Die Modulprüfung wird in mündlicher Form stattfinden. Prüfungstermine sind Dienstag der 11.2.25 und Mittwoch der 12.2.25. Für die Terminvergabe wenden Sie sich bitte an das Sekretariat von Frau Dreibholz
  • Die Übungsblattausgabe wird um eine Woche vorverlegt, so dass Ihnen ab sofort 2 Wochen Bearbeitungszeit zur Verfügung stehen
  • Für die Einschreibung an die Übungsgruppen senden Sie bitte Ihren Namen, Matrikelnummer und Wunschtermin (Mittwoch/Donnerstag) per Mail an den Übungsleiter
  • Für jedwede Fragen wenden Sie sich bitte an den Übungsleiter

Inhalt und Ziele

Viele Vorgänge in den Natur- und Wirtschaftwissenschaften führen auf sogenannte schlechtgestellte inverse Probleme (Wikipedia-Link). Schlechtgestelltheit bedeutet dabei, dass die gesuchte Größe nicht stetig von den vorhandenen Daten abhängt. Ein einfaches Beispiel für Schlechtgestelltheit ist die numerische Differentiation: Ist eine Funktion nur bis auf einen gewissen Mess- oder Approximationsfehler genau bekannt, so wird durch ''naives'' Ableiten der Funktion (etwa durch finite Differenzen) ein vorhandener Messfehler massiv verstärkt – bis hin zur völligen Unbrauchbarkeit des Ergebnisses.

   

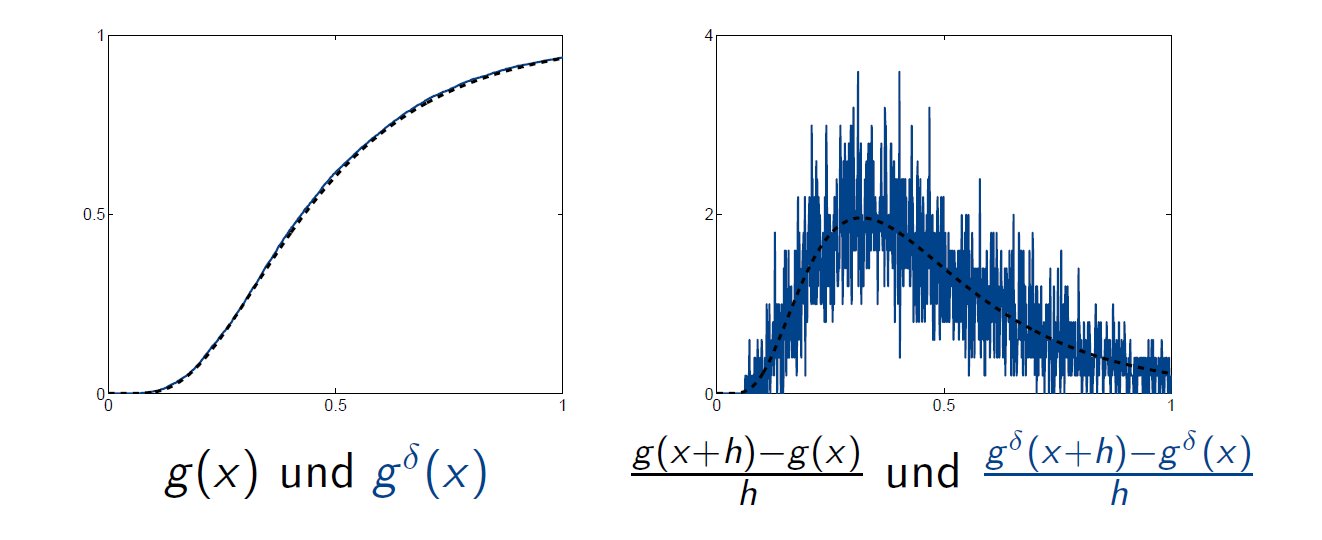Fehlerverstärkung bei numerischer Differentiation

Schlechtgestellte Probleme treten häufig als inverse Probleme zu gutgestellten Problemen auf. So ist etwa die Differentiation das inverse Problem zur gutgestellten Integration, die Messfehler typischerweise reduziert.

An schlechtgestellten Problemen führt in der Praxis oft kein Weg vorbei. Die numerische Differentiation ist z.B. für die Risikobewertung von Finanzderivaten unerlässlich. Typische Quelle schlechtgestellter Probleme sind auch die Parameteridentifikation und neuartige medizinische Tomographiemethoden.

   

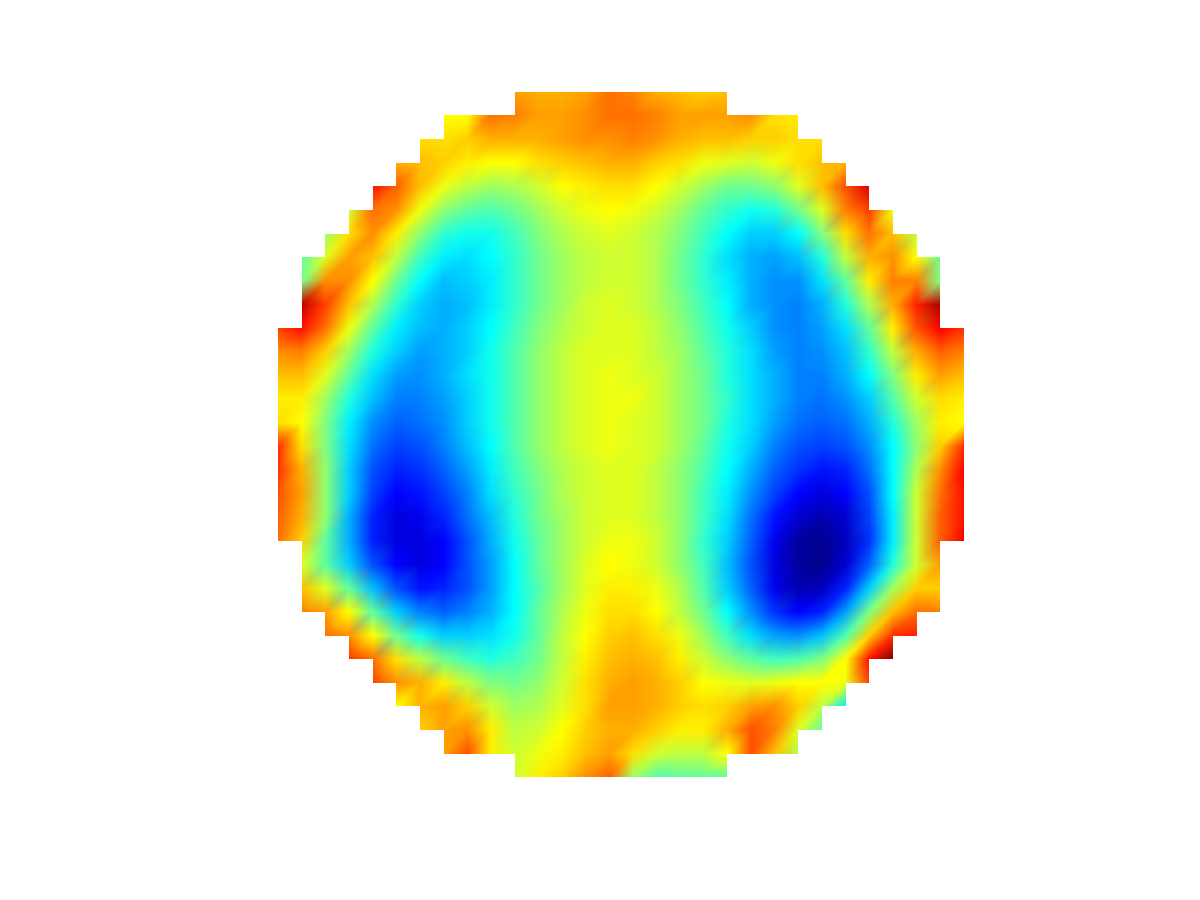Elektrische Impedanz-Tomografie: Schnittbilder der Lunge

In dieser Veranstaltung untersuchen wir, wie inverse Probleme trotz ihrer Schlechtgestelltheit vernünftig (d.h. stabil) gelöst werden können.

Die Veranstaltung richtet sich an Masterstudenten und Bachelorstudenten höheren Semesters. Die benötigten funktionalanalytischen Grundlagen werden in der Vorlesung erarbeitet. Die Vorlesung ergänzt die Veranstaltung "Optimierung und inverse Probleme" aus dem Sommersemester 2024, setzt diese aber nicht voraus und kann auch unabhängig davon gehört werden.

Vorlesung

Die Vorlesung findet in hybrider Form statt. Es werden wöchentlich voraufgezeichnete Vorlesungsvideos im Umfang von ca. 2 SWS zum Selbststudium auf dieser Homepage gelistet. Dazu findet wöchentlich (erstmalig am 15.10.24)

  • Dienstags 14-16 Uhr, Robert-Mayer-Str. 10 - Raum 110

ein Kolloquium ("Fragestunde") in Präsenz statt. Der Übungsbetrieb findet regulär in Präsenz statt.

Übungen

Die Übungen finden in zwei Gruppen, Mittwochs und Donnerstags , 16-18 Uhr c.t., in zweichwöchigem Rythmus, in der Robert-Mayer-Str. 10 - Raum 107 statt. Terminübersicht:

  • Übung 1: Mittwoch und Donnerstag 23/24.10.24
  • Übung 2: Mittwoch und Donnerstag 6/7.11.24
  • Übung 3: Mittwoch und Donnerstag 20/21.11.24
  • Übung 4: Mittwoch und Donnerstag 4/5.12.24
  • Übung 5: Mittwoch und Donnerstag 18/19.12.24
  • Übung 6: Mittwoch und Donnerstag 15/16.01.25
  • Übung 7: Mittwoch und Donnerstag 29/30.01.25

Prüfung

Die Modulprüfung wird in mündlicher Form in der letzten Vorlesungswoche stattfinden. Prüfungstermine sind

  • Dienstag der 11.2.25
  • Mittwoch der 12.2.25

Für die Terminvergabe wenden Sie sich bitte an das Sekretariat von Frau Dreibholz.

Wöchentlicher Plan der Vorlesungsabschnitte

  • 1. Woche: S. 1-4 (Besprechung am 22.10.24)
    • 0.1 Motivation
    • 1 Einleitung
  • 2. Woche: S. 5-9 (Besprechung am 29.10.24)
    • 2.1 Lineare inverse Probleme: Grundbegriffe
  • 3. Woche: S. 9-12 (Besprechung am 05.11.24)
    • 2.2 Unbeschränkte lineare Operatoren
  • 4. Woche: S. 12-16 (Besprechung am 12.11.24)
    • 2.3 Moore-Penrose-Inverse
  • 5. Woche: S. 17-18 (Besprechung am 19.11.24)
    • 2.4.1 Satz von Arzela-Ascoli
  • 6. Woche: S. 19-22 (Besprechung am 26.11.24)
    • 2.4.2 Kompakte Operatoren
    • 2.4.3 Kompaktheit von Integraloperatoren
  • 7. Woche: S. 22-25 (Besprechung am 03.12.24)
    • 2.4.4.1 Quadratische Formen und Hilbertraum-ONBs
  • 8. Woche: S. 25-29 (Besprechung am 10.12.24)
    • 2.4.4.2 Spektralsatz für kompakte Operatoren
    • 2.4.4.3 Singulärwertzerlegung kompakter Operatoren
  • 9. Woche: S. 29-34 (Besprechung am 17.12.24)
    • 2.4.4.4 Singulärwertzerlegung und Moore-Penrose-Inverse
    • 3.1.1 Regularisierung linearer Probleme: Motivation und Definition
  • 10. Woche: S. 34-38 (Besprechung am 14.01.24)
    • 3.1.2 Filter-basierte Regularisierung
    • 3.1.3 Abgeschnittene SWZ und Tikhonov-Regularisierung
  • 11. Woche: S. 38-42 (Besprechung am 21.01.24)
    • 3.2.1 Sätze von Baire, von der gleichmäßigen Beschränktheit und von Banach-Steinhaus
    • 3.2.2 Schwache Konvergenz
  • 12. Woche: S. 42-45 (Besprechung am 28.01.24)
    • 3.3.1 Parameterwahlstrategien
  • 13. Woche: S. 45-50 (Besprechung am 04.02.24)
    • 3.3.2 Das Bakushinskii-Veto
    • 3.4 Diskrepanzprinzip für das Tikhonov-Verfahren

Materialien zur Vorlesung

Evaluation

Personen

Literatur

  • Andreas Rieder: Keine Probleme mit inversen Problemen. Vieweg, Wiesbaden, 2003

Modulzuordnung