12
Fachbereich
Institut für Mathematik
Toggle navigation EN

​

Optimierung und inverse Probleme (SoSe24)

Aktuelles

  • Die Klausureinsicht der Nachklausur findet am Dienstag den 15.10.24 um16-17 Uhr in Raum 103a - RM10 statt.
  • Für jedwede Fragen wenden Sie sich bitte an den Übungsleiter.

Inhalt und Ziele

Die Natur- und Wirtschaftswissenschaften wurden in den letzten Jahrzenten revolutioniert durch die Möglichkeit, das Verhalten eines Systems bei vollständiger Kenntnis aller dazu nötigen Parameter rechnergestützt (numerisch) vorherzusagen. Ziel der numerischen Simulation ist oft die Optimierung des Systems oder die Identifikation der beschreibenden Parameter. In dieser Vorlesung wird eine Einführung in (kontinuierliche) Optimierungs- und Identifikationsalgorithmen gegeben. 

Vorkenntnisse über Optimierung werden nicht vorausgesetzt. Die Vorlesung richtet sich an Bachelor-Studierende ab dem 4. Semester und an Master-Studierende (Modul BaM-NUM-g, MaM-FN-g). Aufbauend auf dieser Vorlesung wird im Wintersemester 2024/25 die Vorlesung Fortgeschrittene Optimierung und inverse Probleme (Modul BaM-NUM-k, MaM-FN-k) angeboten.

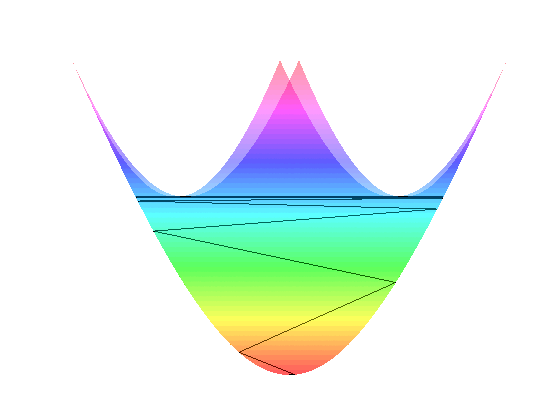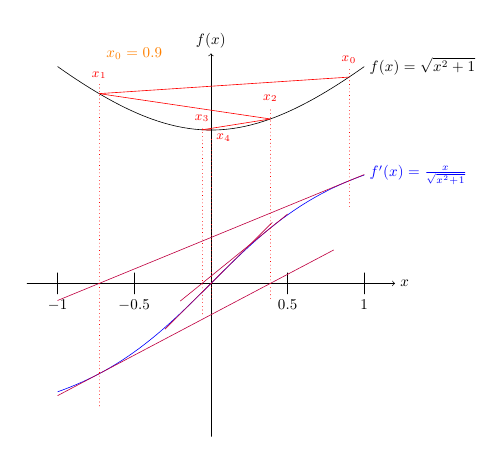
Minimierung einer Zielfunktion durch Anwendung des Newton-Verfahrens auf ihre Ableitung.

Personen

Vorlesung

Die Vorlesung findet in hybrider Form statt. Es werden wöchentlich voraufgezeichnete Vorlesungsvideos im Umfang von ca. 4 SWS zum Selbststudium auf dieser Homepage gelistet. Dazu findet wöchentlich (erstmalig am 16.4.24)

  • Dienstags 14-16 Uhr, Robert-Mayer-Str. 10 - Raum 109c

ein Kolloquium ("Fragestunde") in Präsenz statt. Der Übungsbetrieb findet regulär in Präsenz statt.

Wöchentlicher Plan der Vorlesungsabschnitte

  • 1. Woche: S. 1-12 (Besprechung am 23.04.24)
    • 1.1 Einführung und einfache Beispiele
    • 1.2 Anwendungsbeispiele
    • 2.1.1 Grundlagen und Notationen
  • 2. Woche: S. 12-20 (Besprechung am 30.04.24)
    • 2.1.2 Optimalitätsbedingungen
    • 2.1.3 Konvexität
    • 2.1.4 Konvexität und Optimalität
  • 3. Woche: S. 20-27 (Besprechung am 07.05.24)
    • 2.2.1 Gradientenverfahren
    • 2.2.2 Armijo-Schrittweitenregel
    • 2.2.3 Konvergenz des Gradientenverfahrens
  • 4. Woche: S. 27-32 (Besprechung am 14.05.24)
    • 2.3.1 Konvergenz allgemeiner Abstiegsverfahren
    • 2.3.2a Zulässigkeit der Suchrichtungen
    • 2.3.2b Zulässigkeit der Schrittweiten
  • 5. Woche: S. 32-41 (Besprechung am 21.05.24)
    • 2.3.3 Zulässigkeit der Armijo-Schrittweitenregel
    • 2.3.4 Die Powell-Wolfe-Schrittweitenregel
    • 2.4.1 Neumannsche Reihe und Lemma von Banach
  • 6. Woche: S. 41-51 (Besprechung am 28.05.24)
    • 2.4.2 Newton-Verfahren für Gleichungssysteme
    • 2.4.3 Newton-Verfahren für Optimierungsprobleme
    • 2.4.4a Die Dennis-Moré-Bedingungen
  • 7. Woche: S. 51-58 (Besprechung am 04.06.24)
    • 2.4.4b Inexakte Newton-Verfahren
    • 2.4.5 Quasi-Newton-Verfahren
  • 8. Woche: S. 58-70 (Besprechung am 11.06.24)
    • 2.4.6 Das globalisierte Newton-Verfahren
    • 2.5.1 Das Gauß-Newton-Verfahren
    • 2.5.2 Das Levenberg-Marquardt-Verfahren
  • 9. Woche: S. 71-79 (Besprechung am 18.06.24)
    • 3.1.1 Lineare Optimierung: Motivation und Normalform
    • 3.1.2 Lineare Optimierung: Anwendung aus der Spieltheorie
    • 3.1.3 Lineare Optimierung: Charakterisierung der Lösungen
  • 10. Woche: S. 79-85 (Besprechung am 25.06.24)
    • 3.1.4.1 Simplex-Verfahren: Basisvektoren und Stoppkriterium
    • 3.1.4.2 Simplex-Verfahren: Pivotschritt
  • 11. Woche: S. 85-94 (Besprechung am 02.07.24)
    • 3.2.1a Restringierte Optimierung: Tangentialkegel
    • 3.2.1b Restringierte Optimierung: linearisierter Tangentialkegel
    • 3.2.1c Restringierte Optimierung: Constraint Qualifications
    • 3.2.2a Restringierte Optimierung: Trennungssatz von Hahn-Banach
    • 3.2.2b Restringierte Optimierung: Lemma von Farkas
  • 12. Woche: S. 94-102 (Besprechung am 09.07.24)
    • 3.2.2c Restringierte Optimierung: KKT-Bedingungen
    • 3.2.3 KKT-Bedingungen für konvexe Probleme
    • 3.2.4 Optimalitätsbedingungen zweiter Ordnung
    • 3.2.5 Das Lagrange-Newton-Verfahren
  • 13. Woche: S. 102-110 (Besprechung am 16.07.24)
    • 3.2.6 Ausblick: SQP-Verfahren
    • 3.2.7 Ausblick: Penalty- und Barrier-Verfahren
    • 4. Ausblick: Globale Optimierung

Übungen

Der Übungsbetrieb findet wöchentlich

  • Dienstags 16-18 Uhr, Robert-Mayer-Str. 10 - Raum 110
  • Donnerstags16-18 Uhr, Robert-Mayer-Str. 10 - Raum 110

statt. Erstmalig am 23.4.24, in der zweiten Vorlesungswoche. Für die Anmeldung zu dem Übungsbetrieb kontaktieren Sie den Übungsleiter.

Materialien zur Vorlesung

Evaluation

Übungsblätter

Prüfung

Die schriftliche Klausur findet am Freitag den 19.07.2024 10:00 - 12:00 Uhr im Hörsaaltrakt Bockenheim - H I statt. Falls Sie die Klausur nicht bestanden haben, gibt es die Möglichkeit einen Wiederholungsversuch am Donnerstag den 10.10.2024 um 10-12 Uhr in Raum im Hörsaaltrakt Bockenheim H 14 abzulegen. Für die Prüfung sind alle unbelebten, nicht elektronischen Hilfsmittel und ein einfacher wissenschaftlicher Taschenrechner zugelassen (Taschenrechner, deren Funktionsumfang den des FX-991DE Plus (FX-991DEX, FX-991ES) nicht übersteigt, sind zugelassen). Insbesondere sind damit eigene Notizen, das Skript der Vorlesung, die Übungsaufgaben mitsamt Lösung und Bücher zugelassen.

Prüfungsrelevant sind alle Übungsaufgaben, sowie der Stoff der Vorlesung, siehe Skript. Für die Zulassung zur Modulprüfung sind keine Studienleistungen erforderlich. Wir empfehlen jedoch die Modulprüfung nur dann abzulegen, wenn Sie in den Übungen 50% der Punkte in schriftlichen Aufgaben und Programmieraufgaben erreicht haben. Bei dem Nichtbestehen der Prüfung wird ein Zweittermin individuell vereinbart.

Literatur

  • M. Ulbrich, S. Ulbrich: Nichtlineare Optimierung, Birkhäuser Basel 2012
  • C. Geiger, C. Kanzow: Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben, Springer 1999
  • C. Geiger, C. Kanzow: Theorie und Numerik restringierter Optimierungsaugaben, Springer 2002M
  • Hanke-Bourgeois: Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens, Teubner Verlag, Wiesbaden, 2009

Modulzuordnung

  • Modulkürzel: BaM-NUM-g, MaM-FN-g.
  • Link zur Veranstaltungsseite im Vorlesungsverzeichnis: Vorlesung & Übung.