Spectral properties
In order to understand the behaviour of a many-particle system it is useful to understand how a single particle is affected on average. To do this one can calculate or measure spectral functions. These quantities provide information about how much energy is needed to, e.g., put (or remove) an extra particle into the system in a certain state, or excite a particle already present in the system from one state to another. If the interaction between particles is not small, these properties will strongly depend on the state of the system.
A good example of how important spectral functions are for proper understanding of the behaviour of strongly interacting systems is liquid Helium (4He) below the lambda point (~2.17K) [1]. The dispersion relation (dependence of energy on the momentum) has a very characteristic shape which is linear for small momenta and has a local minimum for higher momenta (roton), Fig. 1. This shape is the key to understanding why the particles contributing to superfluidity do not scatter on the walls of the surrounding container, which results in zero viscosity of the superfluid fraction. This shape also allows to understand other properties of superfluid, like the second sound etc.
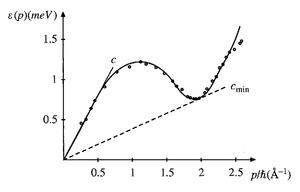
Fig. 1. Dispersion relation of a superfluid Helium-4. Figure taken from Ref. [1].
We are, for example, interested in the spectral functions of a system described by the Bose-Hubbard Hamiltonian, which describes bosons in optical lattice. Lately, the theory of elementary excitations in this model has been intensively studied. Their properties in the Mott insulating phase are quite well understood. We observe two dominant (Hubbard) bands representing particle and hole excitations. Beyond these there are some smaller features, some of which are thermally activated while other are robust with respect to varying temperature [3]. In the superfluid phase the nature of excitations changes dramatically. Instead of particle and hole-like excitations we observe quasi-particles, which arise due to fluctuations of phase and amplitude of the condensate [4], Fig. 2 (c,d). Looking into Fig. 2(a) one can see that the dispersion relation of phase modes (black line) becomes linear for low momenta, just as in case of Helium below the lambda point, hence the name superfluid. However, even knowing this we are still far from fully understanding the spectral properties of the superfluid phase. Especially, the nature of the amplitude mode is elusive. As seen in Fig. 2 the dependence of this mode’s energy on quasi-momentum or on density of particles is highly non-trivial. Even the distribution of the spectral weight between phase and amplitude mode changes dramatically with parameters of the system.


Fig. 2. Spectral properties of the Bose-Hubbard model. [Left panel] Dispersion relations (a), energy dependence on density (b) and pictorial representation of Higgs and amplitude modes (c, d). Ref. [5] [Right panel] Local densities of states of, Ref. [4].
Experimentally many techniques have been developed in order to measure spectral functions. For example the inelastic scattering of high-energy neutrons allows to measure the excitation spectrum and momentum distribution of particles in superfluid Helium [2]. For experiments with cold atoms in optical lattices also techniques similar to angle-resolved photoemission spectroscopy (ARPES) were developed. Using Raman or Bragg spectroscopy we can directly access information about the momentum-resolved one-particle spectrum [1] or the dynamical structure factor [5]. In fact, in Ref. [5] a remarkable agreement between experimental results and theoretical predictions of the quasi-particle theory has been shown.
Theoretical calculation of spectral properties of strongly interacting many-particle systems remains a challenging task. One needs to balance between using an appropriately accurate approximation scheme and feasibility of analytical or numerical calculations. However, with such powerful tools as the quasi-particle theory [4] and dynamical mean-field theory [6-8] we hope to increase our understanding of spectral properties of interacting bosons and fermions in optical lattices.
[1] J. E. Annett, Superconductivity, Superfluids, and Condensates, Oxford University Press, Oxford, 2004.
[2] G. D. Mahan, Many-particle physics 2nd ed., Plenum Press, New York, 1990.
[3] H. U. R. Strand, M. Eckstein, and P. Werner, Phys. Rev. A 92, 063602 (2015).
[4] U. Bissbort, M. Buchhold, and. W. Hofstetter, arXiv 1401.4466 (2014).
[5] U. Bissbort et al., Phys. Rev. Lett. 106, 205303 (2011).
[6] K. Byczuk, and D. Vollhardt, Phys. Rev. B 77, 235106 (2008).
[7] A. Hubener, M. Snoek, and W. Hofstetter, Phys. Rev. B 80, 245109 (2009).
[8] J. Panas, A. Kauch, J. Kuneš, D. Vollhardt, and K. Byczuk, Phys. Rev. B 92, 045102 (2015).





