Hofstetter

Dynamical Mean-Field Theory: from Classical to Quantum mean-field theory

The dynamical mean-field theory (DMFT) is a non-perturbative approach which has been developed during nineties in the context of strongly correlated electronic systems and nowadays is quite successfully implied to describe many physical features of strongly correlated systems, mainly in connections with the Mott transition and high-temperature superconductivity, but also recently in the context of ultracold atomic gases.
The original idea stem from a paper from W. Metzner and D. Vollhardt [1] , who showed that in the limit of infinite dimension (or more precisely very large connectivity), the physics of many-body fermionic systems is highly simplified altough non-trivial. 

It is well known that for a classical system like the Ising model for example, whose Hamiltonian is given by the formula aside, the static mean-field theory, in which all fluctuations are frozen, becomes exact in infinite dimensions. In this case the effect of the other sites on a given site is described by an effective static magnetic field (Weiss field), whose value is fixed by the self-consistency of the approach.           

 

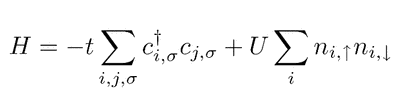
If now one considers in the same limit a quantum system, for example the Hubbard Model whose Hamiltonian is, suitably rescaling the hopping parameter t to ensure a meaningful limit for infinite dimensions, the spatial fluctuations from site to site are frozen like in the classical case, while local quantum fluctuations in time are not. Therefore the same limit is intrinsically richer for a quantum system than for a classicalsystem because local quantum fluctuations are still present in the limit. To describe the local dynamics of electrons jumping from the surrounding lattices sites on a given site, we can still introduce a Weiss field, which however now is a function of time, i.e. a dynamical field. 

 

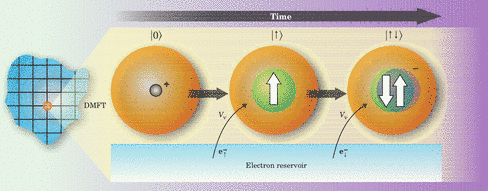
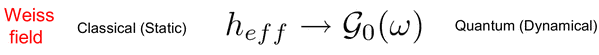
 In the same limit the self-energy, which describe the effect on the interaction on the propagation properties of the particles, loose its momentum dependence and becomes a local object, fully retaining a non-trivial dependence on the frequency. What is however more important to realize is that the uselfulness of these concepts goes far beyond the infinite dimensional case. Indeed, exactly like the static mean-field theory has been successfully used as an  approximate approach to study the properties of classical system in three-dimensional space,  in the same way DMFT can be used as a powerful approximation for 3d quantum systems, i.e. DMFT is exactly a quantum version of classical mean-field theory in the sense that is exact in the same limit. For finite dimensional systems this approximation can be more easily summarized considering the self-energy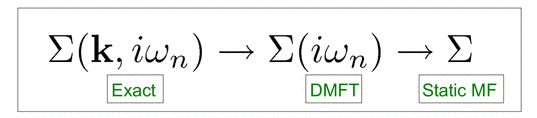, i.e. DMFT amount to neglect the momentum dependence of the self-energy while the static mean-field theoryamounts to neglect also the frequency dependence and therefore is a limit case of DMFT where the self-energy doesn't depend on the momentum.

References:

[1] W. Metzner and D. Vollhardt, Phys. Rev. Lett. 62, 324–327 (1989)

[2] A. Georges et al. , Rev. Mod. Phys. 68, 13–125 (1996)

[3] G.Kotliar and D. Vollhardt, Physics Today, Vol. 3 (2004)

DMFT and cold gases

In the context of cold gases very often the features of the system under investigation are beyond the reach of DMFT as it was originally formulated ( i.e. to address many-body fermionic lattice systems in a uniform environment). Therefore several extensions of DMFT has been developed to describe ultracold gases in optical lattices.

  • In the practice ultracold gases need to be confined,  therefore these systems are in general intrinsically non-homogeneus because of the trapping potential.  To describe this kind of systems, and specifically antiferromagnetic pattern in trapped fermionic gases,  DMFT has been generalized to real-space DMFT (R-DMFT)
  • Since the role of the electronic spin in condensed matter is played by the hyperfine states  of the atomic species under investigation when dealing with ultracold gases, the number of  hyperfine states in general do not have to be restricted to 2 like in spin 1/2 case. Therefore we can go beyond considering multiflavours mixtures with N > 2. which show a rich and interesting physics.  DMFT has been generalized to study multiflavour systems (Work-in-progress) 
  • Ultracold gases are not only composed by Fermions, but also by Bosons or even mixtures of Bosons and Fermions.  Mixtures of Bosons and Fermions can be described using the generalized-DMFT (G-DMFT) which is a combination of bosonic Gutzwiller approach and Fermionic DMFT. Very recently DMFT has been also generalized to address pure bosonic systems (B-DMFT), including fluctuations beyond the Gutzwiller approach, to describe interesting problems like Bosonic magnetism.
  • DMFT has also being used (see here) to study the interplay between strong correlation and disorder in many-body systems  to study interesting phenomena like Anderson localization.