Disordered systems
The physics of solids that are interacting and, at the same time, disordered are currently of general interest in solid-state physics. Mainly, this is due to the fact that most real materials exhibit both features. Essentially, in these systems two major phenomena are brought into contact. On the one hand strong correlations between the interacting particles of the quantum many-body system, which on its own gives rise to fascinating physics like quantum phase transitions. For example, a transition from a metal to an insulator may be triggered by an increasing interaction strength, the so-called Mott transition [1]. On the other hand, a pure single particle - although non-trivial - phenomenon may be induced in disordered systems, the Anderson localization [2]. A particle is coherently backscattered in a disordered potential so that it might be trapped in a finite region of a infinite system. In solids, Anderson localization can lead to a metal-insulator transition depending on the dimensionality of the system.
Although both phenomena are still under investigation in modern research, the basic mechanism is well-understood. In contrast, little is known about systems that combine both effects. From the experimental solid state point of view, this is partially due to the missing possibility of fine-tuning the strength of the interaction and disorder strength in real materials, nor is it possible to isolate one effect. From the theoretical point of view the difficulty arises through the fact that even the "simpliest" theoretical models of disorded and interacting systems cannot be solved exactly in general. Hence, the theorist must stick to approximations, but as the "simple" models realize a poor description of high-complex real materials, the interplay between theory and experiment that might judge the approximations is hindered.
The rapidly developing field of ultracold atoms in optical lattices is considered to be very promising in gaining a deeper understanding into these open issues. An inherent advantage of these systems is the perfect realisation of the mentioned theoretical models, as for example the Anderson-Hubbard hamiltonian, and therefore they allow a quantitative comparison of theoretical predictions and experimental aobservations. Furthermore ultracold atoms in optical lattices can be controlled with big accuracy and most of the theory entering physical parameters can be tuned at will. In general, there are three different approaches to introduce disorder to optical lattices: (i) by superimposing a further laser with incommensurate frequency [3] (ii) by superimpose a optical speckle field [4] and (iii) by loading a second immobile atomic species into the lattice, which realizes a binary disorder potential due to the interatomic interaction [5].
In our group we are interested in describing strongly correlated systems on a non-perturbative level, as many of the interesting phases are not analytically connected with the non-interacting ground state of the system.
Bosons:
We want to address both fundamental questions of the strongly correlated and disordered systems and specific experimental setups in a ultracold atoms framework. For this purpose, we developed the stochastic mean-field theory (SMFT) [6], which extends the Gutzwiller approach to inhomogeneous bosonic systems, encapsulating disorder induced fluctuations of the order parameter on a stochastic level via distribution functions, thereby describing the system in the thermodynamic limit.
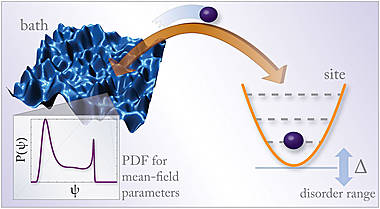 |
In contrast to a simple disorder-averaging of the effective single site or or spatially resolved Gutzwiller theory, the SMFT is capable of describing the Bose glass phase at T=0. At constant particle number and very low temperature the phase diagram
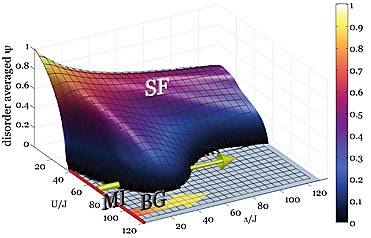 |
exhibits the interesting phenomenon of disorder-induced reentrant superfluidity. Although if applied by individually, both interactions and disorder have a localizing effect, suppressing superfluidity, with the intricate interplay between these two effects, an increase in disorder can actually lead to the formation of a superfluid.
Another interesting question that has been addressed with SMFT is the effect of hopping disorder in addition to on-site disorder in the local energies. At low temperature we find that adding this physical effect to the Bose-Hubbard model actually leads to a stabilization of the superfluid phase, as shown in the phase diagram below.
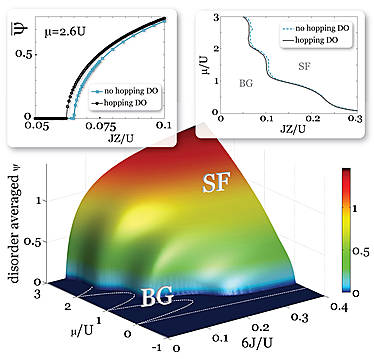 |
Fermions:
The dynamical mean-field theory was very successfull in describing the relevant physics in high dimensional strongly interacting systems. For this reason, recently big effort was made to generalize it to strongly correlated and disordered systems. A breakthrough was achieved by developing the typical mean field theory (TMT) [8], which also allowed for studying the interplay of magnetic long-range order and disorder [9] Whereas the approach is capable of decsribing localization effects it does not account for spatial flucatations due to disorder. These are well described in a fully stochastic description, known as the statistical DMFT [10]. We applied the statistical DMFT to the binary disordered lattice [11], which allowed for the estimation of the paramagnetic groundstate phase diagram. A main finding is the persisting of a novel metal insulator transition, the Mott transition at non-integer filling, in the presence of disorder.
[1] N.F. Mott, Proc. Phys. Soc. A 62, 416 (1949); Metal--Insulator Transitions, 2nd edn. (Taylor and Francis, London 1990).
[2] P.W. Anderson, Phys. Rev. 109, 1492 (1958).
[3] L. Fallani, J.E. Lye, V. Guarrera, C. Fort and M. Inguscio, Phys. Rev. Lett. 98, 130404 (2007).
[4] M. White, M. Pasienski, D. McKay, S.Q. Zhou, D. Ceperley and B. DeMarco, Phys. Rev. Lett. 102, 055301 (2008).
[5] S. Ospelkaus, C. Ospelkaus, O. Wille, M. Succo, P. Ernst, K. Sengstock and K. Bongs, Phys. Rev. Lett. 96, 180403 (2006).
[6] U. Bissbort and W. Hofstetter, EPL 86, (2009) 50007.
[7] U. Bissbort, R. Thomale and W. Hofstetter, arXiv:0911.0923.
[8] K. Byczuk, W. Hofstetter and D. Vollhardt, Phys. Rev. Lett. 94, 056404 (2005).
[9] K. Byczuk, W. Hofstetter and D. Vollhardt, Phys. Rev. Lett. 102, 146403 (2009).
[10] V. Dobrosavljevic and G. Kotliar, Phys. Rev. Lett. 78, 3943 (1997).
[11] D. Semmler, K. Byczuk and W. Hofstetter, Phys. Rev. B 81, 115111 (2010).





