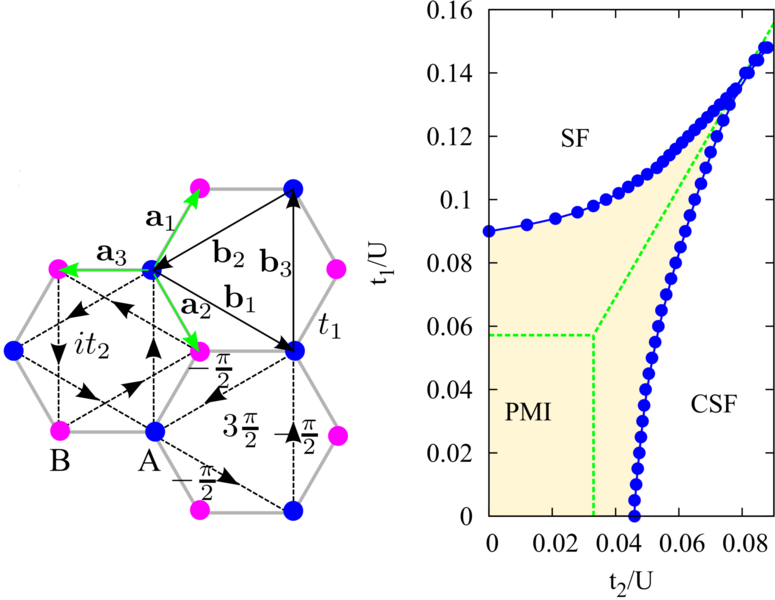
Subproject T3
Interacting and Driven Topological States: Dynamical Mean-Field Study
Prof. Dr. Walter Hofstetter
Institut für Theoretische Physik
Johann Wolfgang Goethe-Universität
Max-von-Laue-Str. 1
60438 Frankfurt / Main
Germany
We will investigate effects of two-particle interactions and periodic driving on topological states of matter of ultracold quantum gases in synthetic gauge fields. Using dynamical mean-field theory (DMFT) and its real-space generalization, we will determine edge mode spectra, many-body topological indices and exotic magnetic order for interacting fermionic and bosonic lattice models in two spatial dimensions. We will investigate the stability of interacting topological bands in the presence of quenched disorder and at finite temperature. Collective excitations of strongly correlated bosons in gauge fields, which may provide further signatures of topological transitions, will be determined by a generalized quasiparticle theory.These investigations will be extended to topological bands, long-range ordered states and generalized topological invariants of multiflavor fermionic systems and Bose-Fermi mixtures in synthetic gauge fields, where we will also be searching for novel phases such as topological supersolids. Interaction effects in periodically driven lattices will be studied by Floquet-Keldysh-DMFT, which can address both the high-frequency forcing limit and Floquet topological insulators at finite frequency. We will calculate the nonequilibrium steady state and its characteristic observables, and determine effective time-independent Floquet-Hamiltonians. We will also investigate generalized topological invariants for interacting driven systems, and effects of micromotion and heating. Finally, the stability of edge modes and topological bands in realistic trapping geometries with soft boundaries, and at interfaces in topological heterostructures, will be investigated. Here we again focus on the effect of two-particle interactions and disorder, study the formation of domains of different topological character via phase separation, and calculate signatures of edge modes in Bragg spectroscopy.