Optimierung und inverse Probleme
Prof. Dr. Bastian von Harrach
M.Sc. Tim Jahn
Aktuelles - Inhalt und Ziele - Personen - Termine - Materialien - Literatur - Modulzuordnung
Aktuelles
- Die Nachprüfungen finden am Mittwoch, den 14.4.2021 zwischen 9:00 und 12:45 Uhr statt. Bitte melden Sie sich über den Übungsleiter an.
- Die Modulprüfung findet in Form mündlicher Prüfungen im Zeitraum 15. bis 18.02.21, jeweils zwischen 9:30 und 12:30 Uhr statt. Bitte melden Sie sich bis zum 15.1.21 bei Frau Gharadaghy an und finden Sie sich am Tag der Prüfung fünf Minuten vor Ihrem Termin am Eingang Robert-Mayer-Str. ein.
- Aktuelle Informationen der Universität zum Umgang mit dem Corona-Risiko finden Sie hier.
- Die Vorlesung findet in digitaler Form ohne Präsenz statt. Es werden wöchentlich (jeweils bis Dienstag, 10 Uhr, beginnend am 03.11.20) Vorlesungsvideos bereit gestellt und unter Termine verlinkt.
- Link zur Übungsanmeldung (aktiv vom 3-10.11.2020).
- Unter Materialien erscheinen wöchentlich (jeweils bis Dienstag 10 Uhr) Übungsblätter. Der Abgabemodus wird unter Übungen erläutert. Es werden Musterlösungen zu den Übungsblättern jeweils bis Dienstag 10 Uhr veröffentlicht. Donnerstags von 10-12 Uhr steht der Übungsleiter für Fragen und Besprechung der Übungsaufgaben und Vorlesung via Zoom zur Verfügung. Die Zugangsdaten erhalten Sie jeweils per Mail.
- Für jedwede Fragen wenden Sie sich bitte an den Übungsleiter.
Inhalt und Ziele
Die Natur- und Wirtschaftswissenschaften wurden in den letzten Jahrzenten revolutioniert durch die Möglichkeit, das Verhalten eines Systems bei vollständiger Kenntnis aller dazu nötigen Parameter rechnergestützt (numerisch) vorherzusagen. Ziel der numerischen Simulation ist oft die Optimierung des Systems oder die Identifikation der beschreibenden Parameter. In dieser Vorlesung wird eine Einführung in (kontinuierliche) Optimierungs- und Identifikationsalgorithmen gegeben. Vorkenntnisse über Optimierung werden nicht vorausgesetzt. Die Vorlesung richtet sich an Bachelor-Studenten ab dem 4. Semester und an Master-Studenten.
 |
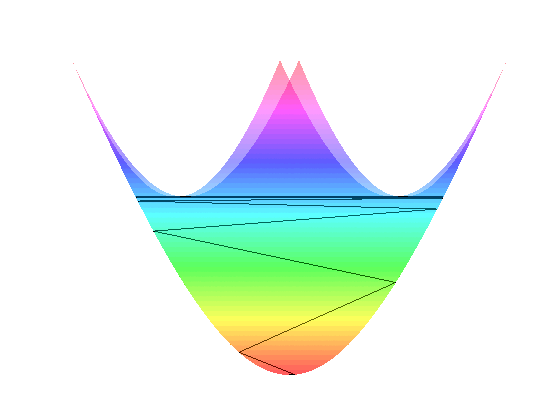 |
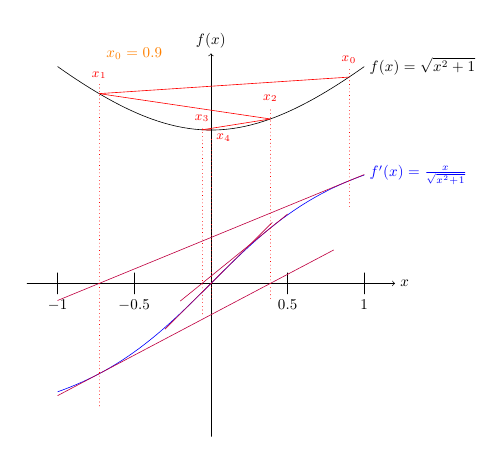
Minimierung einer Zielfunktion durch Anwendung des Newton-Verfahrens auf ihre Ableitung.
Personen
- Prof. Dr. Bastian von Harrach (Dozent)
- M.Sc. Tim Jahn (Übungsleiter)
Termine (Achtung: Bis auf Weiteres entfallen alle Präsenztermine.)
Vorlesung
-
Die Vorlesung findet in digitaler Form ohne Präsenz statt. Es werden wöchentlich beginnend am 03.11.20, jeweils bis Dienstag, 10 Uhr, Vorlesungsvideos bereit gestellt unter den beiden folgenden Links:
- HRZ-Videoportal: Kanal Optimierung und inverse Probleme
- Youtube: Playlist WiSe 2020/21: Optimierung und inverse Probleme
- Musterlösungen zu den Übungsblättern werden dienstags bis 10 Uhr veröffentlicht.
- Die online-Fragestunde findet, beginnend am 12.11.2020, donnerstags von 10-12 Uhr via Zoom statt. Genauere Informationen erhalten Sie per Mail. Zur Abgabe beachten Sie bitte Folgendes:
- Zu schriftlichen Aufgaben ist eine Ausarbeitung anzufertigen.
- Zu Programmieraufgaben ist ein kommentierter MATLAB-Quellcode zu schreiben, welcher die entsprechenden Plots generiert.
- Fügen Sie die eingescannte schriftliche Ausarbeitung sowie den Quellcode und die Plots zu einer einzigen PDF-Datei zusammen und schicken Sie diese bis Dienstag der Folgewoche um 10 Uhr an tutoriumnumerik@math.uni-frankfurt.de. Nutzen Sie dazu Ihre studentische E-Mail-Adresse.
- Zu Votieraufgaben wird keine schriftliche Abgabe verlangt.
- Skript zur Vorlesung: Optimierung_und_inverse_Probleme.pdf (vorläufige Version, wird während der Vorlesungszeit laufend ergänzt und korrigiert)
- Vorlesungsevaluation
- Blatt 1 (Lösungsvorschlag)
- Blatt 2 (Lösungsvorschlag)
- Blatt 3 (Lösungsvorschlag)
- Blatt 4 (Lösungsvorschlag)
- Blatt 5 (Lösungsvorschlag)
- Blatt 6 (Lösungsvorschlag)
- Blatt 7 (Lösungsvorschlag)
- Blatt 8 (Lösungsvorschlag)
- Blatt 9 (Lösungsvorschlag)
- Blatt 10 (Lösungsvorschlag)
- Blatt 11 (Lösungsvorschlag)
- M. Ulbrich, S. Ulbrich: Nichtlineare Optimierung, Birkhäuser Basel 2012
- C. Geiger, C. Kanzow: Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben, Springer 1999
- C. Geiger, C. Kanzow: Theorie und Numerik restringierter Optimierungsaugaben, Springer 2002
- M. Hanke-Bourgeois: Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens, Teubner Verlag, Wiesbaden, 2009
- Modulkürzel: BaM-NUM-g, BaM-NUM-gs, MaM-FN-g, MaM-FN-gs
- Link zur Veranstaltungsseite im Vorlesungsverzeichnis: Vorlesung & Übung.
Übungen
Prüfung
Die Modulprüfung findet in Form mündlicher Prüfungen im Zeitraum 15. bis 18.02.21, jeweils zwischen 9:30 und 12:30 Uhr statt. Bitte melden Sie sich bis zum 15.1.21 bei Frau Gharadaghy an und finden Sie sich am Tag der Prüfung fünf Minuten vor Ihrem Termin am Eingang Robert-Mayer-Str. ein. Prüfungsrelevant sind alle Übungsaufgaben, sowie der Stoff der Vorlesung. Prüfungsrelevant sind alle Übungsaufgaben, sowie der Stoff der Vorlesung (siehe Skript unten) bis einschließlich 3.2.5. Die Abschnitte 3.2.6 und 3.2.7. sowie Kapitel 4 sind nicht Teil der Prüfung. Für die Zulassung zur Modulprüfung sind keine Studienleistungen erforderlich. Wir empfehlen jedoch die Modulprüfung nur dann abzulegen, wenn Sie in den Übungen 50% der Punkte in schriftlichen Aufgaben und Programmieraufgaben erreicht haben. Aktuelle Informationen der Universität zum Umgang mit dem Corona-Risiko finden Sie hier.
Materialien
Vorlesung
Übungsblätter
Literatur





